En el artículo anterior aprendimos qué es una red neuronal y cómo realiza predicciones: la entrada se combina con conocimiento (en forma de un valor de peso) para producir una salida.
En la práctica, solo una entrada y un peso rara vez son de alguna utilidad. La mayoría de los sistemas en el mundo real son mucho más complejos, así que necesitarás redes que puedan manejar múltiples entradas para resolver los desafíos tecnológicos actuales.
Veamos cómo podemos escribir una red neuronal que tome en consideración múltiples datos para lograr mejores estimaciones.
Repaso informal de álgebra lineal: vectores y producto punto
Podemos entender la intuición detrás de la mayoría de los temas de machine learning con muy pocas matemáticas, pero algunos conceptos hacen las cosas mucho más fáciles de entender. Por ahora, solo necesitamos dos ideas: vectores y el producto punto.
Un vector es una lista de números, representada poniéndolos entre corchetes. Simple, ¿verdad?
Todos estos son vectores:
- [1 1] -> Un vector con 2 elementos
- [1 1 3 8] -> Un vector con 4 elementos
- [1 5 7 12 56984 5] -> Un vector con 6 elementos
El tamaño de un vector es el número de elementos que tiene. En los ejemplos de arriba, los vectores son de tamaño 2, 4 y 6 (en orden descendente).
El producto punto es una operación que realizamos en 2 vectores tomando el elemento número n de un vector y multiplicándolo por el elemento número n del otro vector. Después de que terminamos con las multiplicaciones, sumamos los resultados y listo. Es más fácil de entender con un ejemplo.
Supongamos que tenemos dos vectores, [2 3 4] y [5 6 7]. Realizamos el producto punto así:
- Multiplicando el primer elemento de cada vector: 2 * 5 = 10
- Multiplicando el segundo elemento de cada vector: 3 * 6 = 18
- Multiplicando el tercer elemento de cada vector: 4 * 7 = 28
- Sumando todos los resultados anteriores 10+18+28 = 56
- El producto punto de [2 3 4] y [4 5 7] es 56
Es importante recordar que dos vectores necesitan ser del mismo tamaño para que esta operación se aplique. No puedes calcular el producto punto de [1 2] y [2 3 4].
El producto punto es algo importante de saber si quieres aprender más sobre machine learning. Como ejercicio extra, escribamos una implementación simple del producto punto en Python:
def dot_product(first_vector, second_vector):
# Recuerda que solo puedes usar el producto punto con vectores del mismo tamaño
assert( len(first_vector) == len(second_vector))
vectors_size = len(first_vector)
dot_product_result = 0
for index in range(vectors_size):
dot_product_result += first_vector[index] * second_vector[index]
return dot_product_result
Esta pequeña demostración te ayuda a verificar que el código de arriba funciona como se esperaba:
test_vector_one = [2, 3, 4]
test_vector_two = [5, 6, 7]
test_dot_product = dot_product(test_vector_one, test_vector_two)
print("El resultado del producto punto entre los dos vectores de prueba es: {}".format(test_dot_product) )
python3 dot_product_demo.py
El resultado del producto punto entre los dos vectores de prueba es: 56
Bien, ahora que terminamos de refrescar nuestro álgebra lineal, volvamos a las redes neuronales.
Redes neuronales de múltiples entradas
Continuaremos trabajando en el código para nuestra red neuronal. Hasta ahora, nos decía cuántas calorías quemamos después de trotar por una cantidad dada de tiempo.
Como cualquier buen ingeniero, seguimos buscando formas de mejorar nuestro modelo: Investigamos y descubrimos que otros factores influyen en cuántas calorías quemamos mientras trotamos, como la velocidad (en m/s) y la masa del corredor (en kg).
Las redes neuronales pueden tomar en consideración múltiples entradas para realizar una predicción. Cada entrada tendrá un peso específico asociado con ella, y la red realizará una suma ponderada. Las entradas serán multiplicadas por sus respectivos pesos, y los resultados serán sumados juntos para producir la salida.
En nuestro ejemplo anterior, un peso de 7.56 fue aplicado a la entrada de minutos. Nuestra nueva red neuronal tendrá pesos adicionales para velocidad y masa, para un total de 3 pesos.
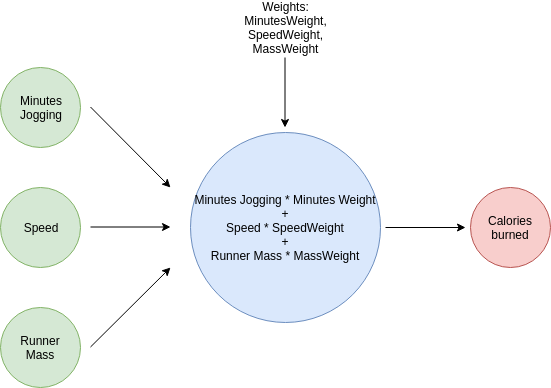
Con investigación pseudo-científica, descubrimos que:
- El valor del peso asociado con el número de minutos trotando es 6.2
- El valor del peso asociado con la velocidad de trote es 8.1
- El valor del peso asociado con la masa del corredor es 0.31
Esta es la versión en Python de nuestra red neuronal predictora de calorías:
# Ahora, input e information son ambos arreglos de números
def multi_input_neural_network(input_information, weights):
assert( len(input_information) == len(weights))
calories_burned = 0
for index in range(len(weights)):
calories_burned += input_information[index] * weights[index]
return calories_burned
También podemos escribir una demostración corta para mostrar cómo usarla:
#DEMO
# Inputs es un arreglo, ordenado como: minutos trotando --> velocidad de trote ---> masa del corredor
# Minutos trotando: 30
# Velocidad de trote: 3 m/s
# Masa del corredor: 80kg
inputs = [30, 3, 80]
# El arreglo de pesos sigue el mismo orden
calculated_weights = [6.2, 8.1, 0.31]
calories_burned = multi_input_neural_network(inputs, calculated_weights )
print("Según mi red neuronal, quemé {} calorías".format(calories_burned))
python3 multiple_input_nn.py
Según mi red neuronal, quemé 235.10000000000002 calorías
Espera un segundo, ¿no es eso un producto punto?
Sí, me alegra que lo hayas notado.
Si pones atención a la implementación de la red neuronal de múltiples entradas, notarás que la suma ponderada es un producto punto entre las entradas y los pesos.
Ahora que lo notaste, podemos re-implementar nuestra red neuronal de múltiples entradas usando la función de producto punto que implementamos antes:
def multi_input_neural_network(input_information, weights):
calories_burned = dot_product(input_information, weights)
return calories_burned
¡Limpio y bonito!
Nota: En la práctica, no necesitas crear tus propias implementaciones para el producto punto o para redes neuronales. Hay librerías con implementaciones de alto rendimiento y bien probadas por ahí. Nuestras implementaciones están destinadas a ilustrar los principios, pero crear tu propia librería de machine learning para uso en producción es algo que podrías no querer hacer todavía.
Una red más grande: múltiples entradas y múltiples salidas
¡Las redes neuronales también pueden generar múltiples estimaciones!
Anteriormente, aprendimos cómo combinar múltiples entradas con un vector de pesos para crear una estimación, algo que podemos visualizar como:
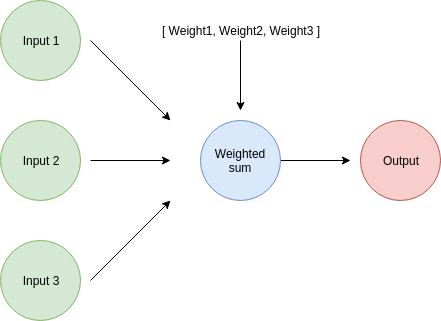
Para estimar múltiples salidas, realizamos sumas ponderadas con un conjunto diferente de pesos para cada nueva salida que necesitamos. Cada predicción tiene su propio vector asociado de pesos. Por ejemplo, si queremos estimar 3 salidas, necesitamos 3 conjuntos de pesos.
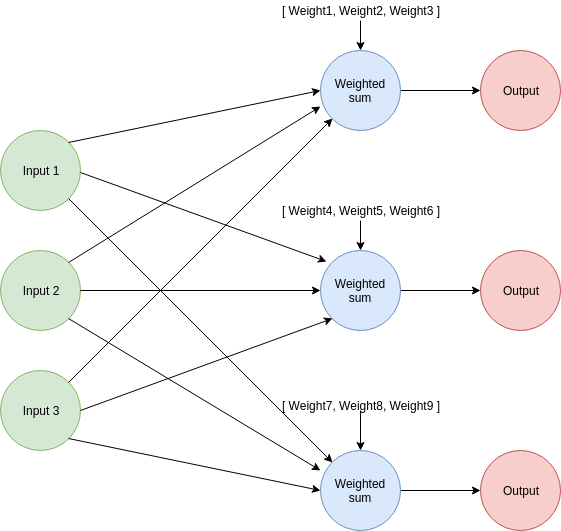
Con esta información, veamos cómo podemos usar esta red para resolver un problema práctico. Supongamos que queremos usar la información que ya tenemos para predecir cuántos días extra viviré gracias a mis sesiones de trote y cuánto dinero ahorraré en medicamentos, además de las calorías quemadas.
Para resumir, nuestra red neuronal ahora tiene:
Entradas:
- Número de minutos trotando
- Velocidad de trote
- Masa del corredor
Salidas:
- Cantidad de calorías quemadas
- Días de esperanza de vida extendida debido a actividad física
- Dinero ahorrado en medicamentos para el corazón.
Pesos:
- Un vector de pesos para la estimación de calorías.
- Un vector de pesos para la estimación de días extra.
- Un vector de pesos para la estimación de ahorros.
![]()
Tres sumas ponderadas tendrán lugar, una para cada una de las salidas. Puede parecer un poco complicado, pero la implementación es directa una vez que entiendes lo que está pasando.
def dot_product(first_vector, second_vector):
assert( len(first_vector) == len(second_vector))
vectors_size = len(first_vector)
dot_product_result = 0
for index in range(vectors_size):
dot_product_result += first_vector[index] * second_vector[index]
return dot_product_result
def multi_input_multi_output_neural_network(input_information, weights):
# Las estimaciones serán puestas y devueltas en un arreglo
estimates = []
for weights_for_estimate in weights:
estimates.append( dot_product(input_information, weights_for_estimate) )
return estimates
#DEMO
# Inputs es un arreglo, ordenado como: minutos trotando --> velocidad de trote ---> masa del corredor
# Minutos trotando: 30
# Velocidad de trote: 3 m/s
# Masa del corredor: 80kg
inputs = [30, 3, 80]
# Pesos para cada una de las 3 salidas
weights_for_calories = [6.2, 8.1, 0.31]
weights_for_extra_days = [0.00407, 0.00618, 0.00303]
weights_for_savings = [0.11, 0.23, 0.06]
# Combinamos todos los pesos en un solo arreglo para ser enviado a la función de estimación de la red neuronal
all_weights = [weights_for_calories, weights_for_extra_days, weights_for_savings]
# El orden de los resultados es el mismo que el orden de los pesos: calorías -> días extra -> dinero ahorrado
estimates = multi_input_multi_output_neural_network(inputs, all_weights )
print("Según mi red neuronal, quemé {} calorías".format(estimates[0]))
print("Según mi red neuronal, viviré {} días extra".format(estimates[1]))
print("Según mi red neuronal, ahorré {} unidades monetarias en medicamentos para el corazón".format(estimates[2]))
Las redes neuronales de múltiples entradas/salidas pueden parecer un poco intimidantes al principio, pero son solo extensiones de cosas que ya conocemos. La mayoría de los conceptos de machine learning son similares: al principio, parecen complicados, pero en realidad son una amalgama de ideas subyacentes muy simples.
Espero que este artículo te haya ayudado a entender las redes neuronales con múltiples entradas y salidas. Ahora que sabemos cómo funciona el proceso de estimación, podemos enfocarnos en aprender los mecanismos que usan las redes para ajustar los valores de sus pesos.
Qué hacer a continuación
- Comparte este artículo con amigos y colegas. Gracias por ayudarme a llegar a personas que podrían encontrar útil esta información.
- Puedes encontrar el código fuente para esta serie aquí
- Este artículo está basado en el libro: Grokking Deep Learning y en Deep Learning (Goodfellow, Bengio, Courville).
- Envíame un email con preguntas, comentarios o sugerencias (está en la página Autor)
