En el artículo anterior, aprendimos sobre el aprendizaje caliente/frío.
También aprendimos que el aprendizaje caliente/frío tiene algunos problemas: es lento y propenso a sobrepasar el objetivo, así que necesitamos una mejor forma de ajustar los pesos.
Un mejor enfoque debería tomar en consideración qué tan precisas son nuestras predicciones y ajustar los pesos en consecuencia. Las predicciones que están muy desviadas resultan en ajustes grandes y las buenas predicciones las cambian solo un poquito.
Necesitamos encontrar una forma de tomar en consideración el error en la predicción cuando calculamos el factor de ajuste para un peso. Lo primero que necesitaremos es entender cómo el valor de un peso específico afecta el error resultante.
Entender esta relación nos ayudará a encontrar una forma de reducir el error ajustando los pesos de nuestra red.
Aprendiendo cómo el peso afecta el error
¿Recuerdas el código que usamos para calcular errores en el artículo anterior?
error = (predicted_value - expected_value)**2
Necesitamos encontrar una relación entre peso y error, y esta expresión es un buen comienzo. ¿Recuerdas de dónde venía predicted_value? Sí, es el valor predicho por la red neuronal para una entrada dada, calculado como:
predicted_value = input * weight
Podemos reemplazar el segundo valor en la primera expresión y obtener:
error = (input * weight - expected_value)**2
O si prefieres la forma de ecuación:
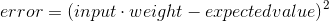
Esta ecuación explica cómo el valor de un peso específico afecta el error. Ya conocemos el valor de input y expected_value de nuestro conjunto de entrenamiento (el conjunto de [entrada, valor_esperado] que usamos para entrenar la red).
Para este ejemplo, supongamos que solo tenemos un par de valores, con una entrada de 0.2 y un valor estimado de 8.
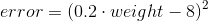
Si graficas esta ecuación, este es el resultado:
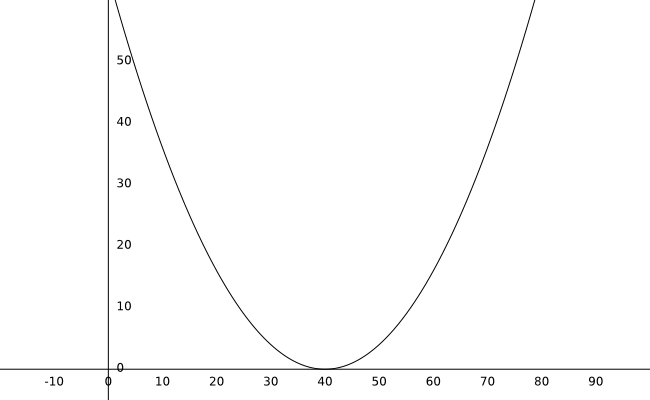
Con un peso inicial de 10, podemos calcular el error como 36 (el punto rojo en la gráfica).
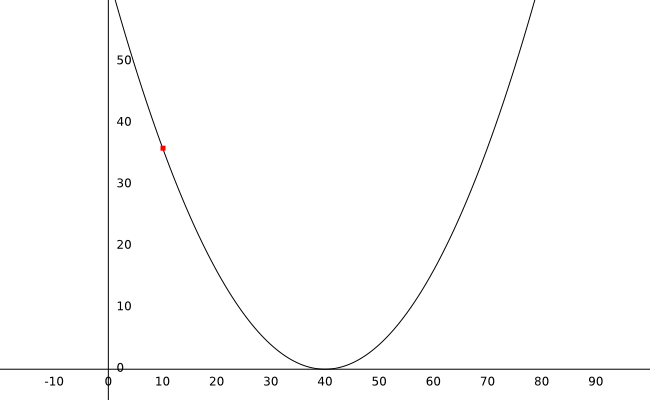
Antes de proceder, necesitamos aprovechar el poder de una de las herramientas matemáticas más útiles: las derivadas.
¿Qué tan sensible es una variable al cambio en otra variable?
Una derivada me dice cuánto cambia una variable en respuesta a un cambio en otra variable. Esta es una medida de qué tan sensible es una variable a los cambios en otra.
Estrictamente hablando:
La derivada de una función nos da la pendiente de la línea tangente a la función en cualquier punto de la gráfica.
Pero no estamos aquí para un curso de cálculo, todo lo que necesitas saber es que podemos usar el valor de la derivada para entender la tasa de cambio entre dos variables.
Recuerda que estamos buscando una forma de actualizar el peso en proporción al valor del error. Si el peso produce un error grande, necesitamos realizar un cambio considerable. Si estamos obteniendo un error con un valor cercano a 0, necesitamos solo un pequeño ajuste.
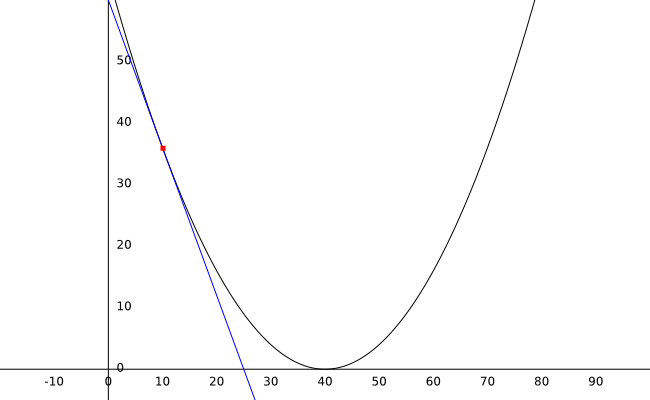
Las derivadas son útiles para esta tarea porque en este caso, su valor es proporcional a qué tan cerca estamos de lograr el error más bajo posible. Mientras más nos acercamos al fondo de la curva (donde el error es 0), más paralela al eje x se vuelve la tangente y menor el valor de la derivada.
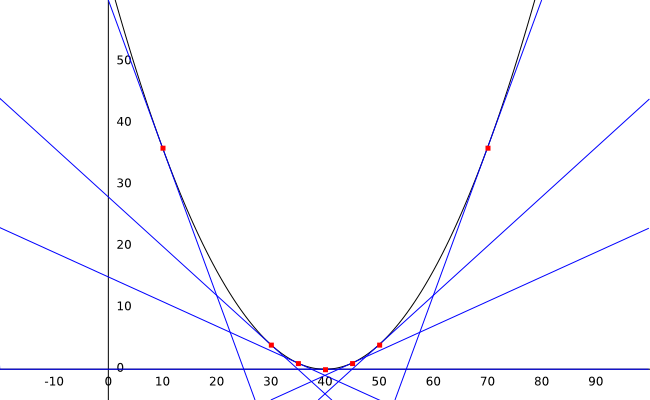
Observa la gráfica de arriba y pon atención al valor de la pendiente de la línea (la derivada) en diferentes puntos.
- En peso:10 el valor de la derivada es -2.4
- En peso:30 el valor de la derivada es -0.8
- En peso:35 el valor de la derivada es -0.4
- En peso:40 el valor de la derivada es 0
- En peso:45 el valor de la derivada es 0.4
- En peso:50 el valor de la derivada es 0.8
- En peso:70 el valor de la derivada es 2.4
Mira la tendencia en los valores: Si nuestro peso está a la izquierda de la curva, el valor de la derivada será negativo. Si el peso está en el lado derecho, el valor de nuestra derivada será positivo. También, mientras más lejos estemos, más alto será el valor.
Así que, para resumir, una derivada me dice toda esta información:
- Si estamos lejos del fondo de la curva, el valor de la derivada será grande.
- Si estamos cerca del fondo de la curva, el valor de la derivada será pequeño.
- Si la derivada es negativa (estamos en el lado izquierdo de la curva), necesitamos aumentar el valor del peso.
- Si la derivada es positiva (estamos en el lado derecho de la curva), necesitamos disminuir el valor del peso.
Usemos esta información para actualizar nuestros pesos de una manera más inteligente.
Implementando descenso de gradiente en Python
La técnica que usaremos se llama descenso de gradiente. Usa la derivada (el gradiente) para descender por la pendiente de la curva hasta que alcancemos el valor de error más bajo posible. Implementaremos el algoritmo paso a paso en Python.
¿Cuál es el valor de nuestra derivada?
Lo primero que necesitamos es calcular la derivada. La derivada de nuestra ecuación de error con respecto al peso está dada por:
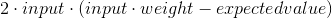
Ahora, esta ecuación necesita dos ajustes antes de que podamos implementarla, solo por conveniencia:
- Ya sé que input*weight = valor predicho, así que usaré eso en la ecuación en su lugar.
- Nos desharemos del 2 que multiplica la expresión. Solo nos importan las otras partes de la ecuación. Más tarde usaremos un factor especial para escalar el valor de nuestra derivada, como resultado, ese 2 no es necesario.
La ecuación para la derivada que usaremos es:
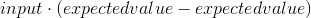
O, en Python:
derivative = input * (predicted_value - expected_value)
Escálala usando Alpha
Recuerda del último artículo que a veces los ajustes en el valor del peso pueden sobrepasar el objetivo. Si el ajuste es demasiado grande corremos el riesgo de ejecutar un bucle de ajuste infinito. Si el valor es demasiado pequeño comparado con los otros parámetros, nuestro proceso de aprendizaje será demasiado lento.
Para arreglar esto, escalaremos el ajuste usando alpha, un número que nos ayuda a regular la tasa de aprendizaje y proteger el código de sobrepasar el objetivo o de ir demasiado lento. Este valor se elige experimentalmente: prueba diferentes órdenes de magnitud (…, 10, 1, 0.1, 0.01, 0.001, …) hasta que encuentres el correcto.
En python, este escalamiento puede implementarse como:
alpha = 18
weight_adjustment = alpha * derivative
¿Sumarlo o restarlo del peso?
Ahora que tenemos un factor de ajuste, ¿deberíamos sumarlo o restarlo de nuestro peso?
Recuerda el resumen que escribimos arriba:
- Si la derivada es negativa (estamos en el lado izquierdo de la curva), necesitamos aumentar el valor del peso.
- Si la derivada es positiva (estamos en el lado derecho de la curva), necesitamos disminuir el valor del peso.
Así que, un valor de derivada negativo debería aumentar el peso, mientras que un valor positivo debería reducirlo. Esto significa que deberíamos restarlo de nuestro peso.
En Python, se vería así:
weight -= weight_adjustment
Implementación final
Juntando todo en una demo completa, nuestro archivo final tiene estos contenidos:
def neural_network(input, weight):
predicted_value = input * weight
return predicted_value
input = 0.2
expected_value = 8
weight = 10
while True:
# Debido a cómo python maneja punto flotante, redondeamos los valores
predicted_value = round(neural_network(input, weight), 2)
print("Según mi red neuronal, el resultado es {}".format(predicted_value))
error = (predicted_value - expected_value)**2
print("El error en la predicción es {} ".format(error))
derivative = input * (predicted_value - expected_value)
print("El valor de nuestra derivada en peso={} es {}".format(weight, derivative))
alpha = 18
weight_adjustment = alpha * derivative
weight -= weight_adjustment
print("El nuevo valor de nuestro peso es {}".format(weight))
print("\n")
if(error == 0):
break
Si ejecutas este código, obtendrás los siguientes resultados:
Según mi red neuronal, el resultado es 2.0
El error en la predicción es 36.0
El valor de nuestra derivada en peso=10 es -1.2000000000000002
El nuevo valor de nuestro peso es 31.6
Según mi red neuronal, el resultado es 6.32
El error en la predicción es 2.822399999999999
El valor de nuestra derivada en peso=31.6 es -0.33599999999999997
El nuevo valor de nuestro peso es 37.648
Según mi red neuronal, el resultado es 7.53
El error en la predicción es 0.22089999999999976
El valor de nuestra derivada en peso=37.648 es -0.09399999999999996
El nuevo valor de nuestro peso es 39.34
Según mi red neuronal, el resultado es 7.87
El error en la predicción es 0.01689999999999997
El valor de nuestra derivada en peso=39.34 es -0.02599999999999998
El nuevo valor de nuestro peso es 39.808
Según mi red neuronal, el resultado es 7.96
El error en la predicción es 0.001600000000000003
El valor de nuestra derivada en peso=39.808 es -0.008000000000000007
El nuevo valor de nuestro peso es 39.952
Según mi red neuronal, el resultado es 7.99
El error en la predicción es 9.999999999999574e-05
El valor de nuestra derivada en peso=39.952 es -0.0019999999999999575
El nuevo valor de nuestro peso es 39.988
Según mi red neuronal, el resultado es 8.0
El error en la predicción es 0.0
El valor de nuestra derivada en peso=39.988 es 0.0
El nuevo valor de nuestro peso es 39.988
Puedes ver cómo los primeros ajustes al peso cambian el valor mucho (de 10 a 31.6). Puedes jugar con el valor de alpha para ver si puedes acelerar el proceso de aprendizaje sin causar sobrepaso. Un alpha=25, por ejemplo, produce la siguiente salida:
Según mi red neuronal, el resultado es 2.0
El error en la predicción es 36.0
El valor de nuestra derivada en peso=10 es -1.2000000000000002
El nuevo valor de nuestro peso es 38.800000000000004
Según mi red neuronal, el resultado es 7.76
El error en la predicción es 0.0576000000000001
El valor de nuestra derivada en peso=38.800000000000004 es -0.04800000000000004
El nuevo valor de nuestro peso es 39.952000000000005
Según mi red neuronal, el resultado es 7.99
El error en la predicción es 9.999999999999574e-05
El valor de nuestra derivada en peso=39.952000000000005 es -0.0019999999999999575
El nuevo valor de nuestro peso es 40.00000000000001
Según mi red neuronal, el resultado es 8.0
El error en la predicción es 0.0
El valor de nuestra derivada en peso=40.00000000000001 es 0.0
El nuevo valor de nuestro peso es 40.00000000000001
¡Ves! mucho más rápido que alpha=18. Sin embargo, alpha=35 causa que la corrección sobrepase el objetivo y el código hace bucles para siempre.
Puntos clave
El descenso de gradiente es un concepto muy importante en muchos algoritmos de ML. Puede ser difícil de entender al principio, pero espero que después de leer este artículo esté mucho más claro.
Algunas de las cosas que necesitas recordar sobre esta técnica son:
- Las derivadas nos dicen cuánto cambia una variable en respuesta a un cambio en otra variable.
- Al encontrar la relación entre peso y error, tratamos de encontrar una forma de minimizar el error cambiando el valor del peso.
- Puedes usar el valor de la derivada para saber en qué lado de la curva y qué tan lejos del fondo (el error mínimo) estás.
- Al usar la derivada (escalada por alpha) puedes actualizar el valor de tu peso en un proceso iterativo que te acercará al error mínimo.
- Elegir un buen valor para alpha es importante: muy pequeño puede resultar en aprendizaje lento, y muy grande puede resultar en sobrepaso.
También puedes entrenar múltiples pesos
En este artículo, estudiamos una versión simplificada del descenso de gradiente con solo un peso. En el siguiente artículo, exploraremos una versión generalizada que nos permitirá entrenar redes con cualquier número de entradas y salidas.
¡Gracias por leer!
Qué hacer después
- Comparte este artículo con amigos y colegas. Gracias por ayudarme a llegar a personas que podrían encontrar útil esta información.
- Puedes encontrar un gran repaso sobre derivadas aquí.
- Este artículo está basado en el libro: Grokking Deep Learning y en Deep Learning (Goodfellow, Bengio, Courville).
- Puedes encontrar el código fuente para esta serie aquí
- Envíame un email con preguntas, comentarios o sugerencias (está en la página Autor)
