MAE y RMSE son algunas de las métricas de error más comunes para problemas de regresión.
A pesar de ser usadas para la misma tarea (entender los errores en tus predicciones) hay diferencias importantes entre las dos. Elegir las métricas correctas para tu modelo puede hacer una diferencia enorme en tu habilidad para resolver un problema.
Los algoritmos que usarás para crear modelos usan la métrica de error para realizar optimizaciones. Tu elección de métrica de error afectará el modelo final y la forma en que evalúas su rendimiento, así que es importante entender la diferencia entre métricas de error.
MAE y RMSE son ambas extremadamente comunes en la práctica, por eso hablaremos de ellas en este artículo. Antes de empezar, tengamos un repaso rápido:
Un modelo de regresión es un modelo que predice un valor continuo. La forma más común de entrenar un modelo de regresión es usando aprendizaje supervisado: tienes un conjunto de ejemplos con las ‘respuestas correctas’. Usas este conjunto de entrenamiento para enseñar al modelo cómo producir esas respuestas con un conjunto de entradas con la esperanza de encontrar reglas generales que puedas aplicar fuera del conjunto de entrenamiento.
Error Absoluto Medio (MAE)
El error absoluto medio (MAE) se define como la suma del valor absoluto de las diferencias entre todos los valores esperados y los valores predichos, dividida por el número total de predicciones. En forma de ecuación, se ve así:
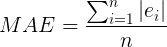
Los valores esperados son las respuestas que ya conoces que son parte de los conjuntos de entrenamiento, validación o prueba, y los valores predichos son los resultados predichos por el modelo para dichas entradas.
Por ejemplo, supón que ejecutas tu modelo en un conjunto de validación y obtienes el siguiente resultado:
| Valor esperado | Valor predicho |
|---|---|
| 5 | 10 |
| 11 | 19 |
| 37 | 32 |
| 9 | 9 |
| 21 | 30 |
| 48 | 43 |
| 33 | 21 |
| 25 | 22 |
| 12 | 15 |
Cada fila en la tabla representa una predicción y su valor esperado asociado.
Por ejemplo, en la primera predicción, la respuesta correcta es 5, pero nuestro modelo predijo un 10, la predicción se desvía por 5. En la tercera predicción, nuestro modelo predijo un 32, donde la respuesta correcta es 37, la predicción se desvía por -5.
Puedes resumir esto en otra tabla con los resultados del error para cada predicción.
| Valor esperado | Valor predicho | Error |
|---|---|---|
| 5 | 10 | 5 |
| 11 | 19 | 8 |
| 37 | 32 | -5 |
| 9 | 9 | 0 |
| 21 | 30 | 9 |
| 48 | 43 | -5 |
| 33 | 21 | -12 |
| 25 | 22 | -3 |
| 12 | 15 | 3 |
¿Cómo calculamos el error absoluto medio?
Fácil, solo promedia el valor absoluto de los errores. Con los datos de nuestra tabla, sería así:
MAE = (|5|+|8|+|-5|+|0|+|9|+|-5|+|-12|+|-3|+|3|)/9 = (5+8+5+0+9+5+12+3+3)/9 = 50/9 =~ 5.55
Te podrías estar preguntando por qué usamos valores absolutos. Esto es importante para tomar en consideración el hecho de que tenemos dos tipos de errores:
- El valor predicho es menor que el valor esperado.
- El valor predicho es mayor que el valor esperado.
El valor absoluto asegura que ambos tipos contribuyan al error general. Sin él, los errores positivos y negativos se cancelarían entre sí. Esto es malo: tu modelo de regresión podría funcionar terriblemente y aún así devolver un error general muy bajo.
Para ilustrar este punto, repite el cálculo para el error total usando los datos en la tabla, pero esta vez no uses los valores absolutos:
Error Total = (5 + 8+ -5 + 0 + 9 + -5 + -12 + -3 + 3)/9 = 0
Sí, un valor total de 0 a pesar de cometer varios errores.
MAE es una métrica muy simple y útil para el error, y ahora sabes casi todo lo que hay que saber sobre ella.
Hablemos sobre RMSE.
Error Cuadrático Medio (RMSE)
RMSE se define como la raíz cuadrada del promedio de los errores al cuadrado. En forma de ecuación, se ve así:
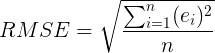
No te preocupes si eso suena un poco confuso, es mucho más fácil de entender con un ejemplo. Calculémoslo, paso a paso, usando la misma tabla de errores de antes.
- Paso 1: Eleva al cuadrado los valores de error
| Error | Error al cuadrado |
|---|---|
| 5 | 25 |
| 8 | 64 |
| -5 | 25 |
| 0 | 0 |
| 9 | 81 |
| -5 | 25 |
| -12 | 144 |
| -3 | 9 |
| 3 | 9 |
- Paso 2: Suma los errores al cuadrado y divide el resultado por el número de ejemplos (calcula el promedio)
MSE = (25 + 64 + 25 + 0 + 81 + 25 + 144 + 9 + 9)/9 =~ 42.44
- Paso 3: Calcula la raíz cuadrada del promedio
RMSE = raíz_cuadrada(42.44) =~ 6.51
Calcular tanto el MAE como el RMSE es bastante simple, y ambos resumen el error total como un solo número. Ahora que sabemos cómo calcular ambos, discutamos sus principales diferencias y cuándo usar cada uno.
¿MAE o RMSE?
Primero, enlistemos las cosas que ambos tienen en común:
- Ambos se usan para medir el error producido por un modelo predictivo.
- Ambos son rápidos y fáciles de calcular.
- Ambos resumen el error como un solo valor numérico que es fácil de entender.
La principal diferencia entre las dos métricas es la contribución de valores individuales de error al resultado final.
En el caso de MAE, la contribución sigue un comportamiento lineal. Esto significa que un error de 10 contribuye el doble que un error de 5. Un error de 1000 contribuye 10 veces más que un error de 100.
RMSE tiene un comportamiento diferente: debido a la operación de elevar al cuadrado, valores muy pequeños (entre 0 y 1) se vuelven aún más pequeños, y valores más grandes se vuelven aún más grandes. Esto significa que valores de error grandes se magnifican, mientras que los pequeños se ignoran.
Si fueses a graficar la contribución de valores individuales al error en nuestro ejemplo, MAE y RMSE seguirían un comportamiento como el siguiente:
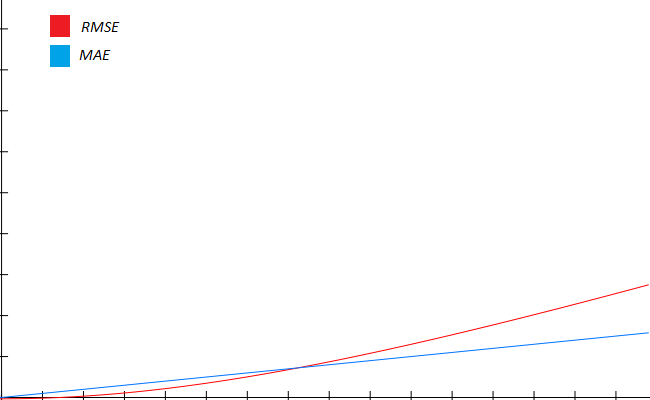
En resumen, quieres usar MAE para problemas donde el error empeora linealmente, como un modelo que predice pérdida monetaria. Un error de $100 es el doble de malo que un error de $50. MAE no tiene una predilección por errores pequeños o errores grandes.
RMSE se usa cuando errores pequeños pueden ser ignorados con seguridad y errores grandes deben ser penalizados y reducidos tanto como sea posible. RMSE da mucha más importancia a errores grandes, así que los modelos tratarán de minimizar estos tanto como sea posible.
MAE y RMSE son ambos conceptos muy simples e importantes, y ahora estás un paso más adelante en tu alfabetización en ciencia de datos.
Espero que esta información sea útil en tu vida profesional.
¡Gracias por leer!
Qué hacer después
- Comparte este artículo con amigos y colegas. Gracias por ayudarme a llegar a personas que podrían encontrar útil esta información.
- Este artículo está basado en el libro: Data Science for Business: What You Need to Know about Data Mining and Data-Analytic Thinking.
- Envíame un email con preguntas, comentarios o sugerencias (está en la página Autor)
