En el artículo anterior aprendimos cómo usar Keras para construir redes neuronales más poderosas. Las bibliotecas de grado profesional como Keras, Tensorflow y Pytorch te permiten construir redes neuronales que pueden aprender patrones intrincados y resolver problemas novedosos.
Las redes de deep-learning permiten aprender patrones sutiles gracias a su espacio de hipótesis inherentemente grande, pero esto trae un nuevo problema: sobreajuste. Las redes neuronales son propensas al sobreajuste, así que es importante conocer los fundamentos de la regularización.
¿Qué es la regularización? Es un conjunto de técnicas usadas para aliviar el problema del sobreajuste. En este artículo, aprenderemos cómo detectar y arreglar el sobreajuste en nuestras redes neuronales.
Si no estás familiarizado con los términos sobreajuste y conjuntos de validación/prueba, echa un vistazo a estos artículos antes de proceder:
Bien, ¡empecemos!
Detectando sobreajuste
Usaremos una configuración muy similar a la que usamos en el artículo anterior: Una RN de Keras que trata de clasificar el conjunto MNIST de dígitos escritos a mano.
# Importar tensorflow y Keras
import tensorflow as tf
from tensorflow import keras
# Importar bibliotecas de apoyo para operaciones matriciales y gráficos
import numpy as np
import matplotlib.pyplot as plt
# Obtener el dataset MNIST
from keras.datasets import mnist
(x_train, y_train), (x_test, y_test) = mnist.load_data()
# Escalar las entradas
x_train = x_train / 255.0
x_test = x_test / 255.0
Esta parte es la misma que en el último artículo.
Ahora extraeremos nuestro conjunto de validación de los ejemplos de entrenamiento. Para hacer los efectos del sobreajuste más visibles, entrenaremos la red usando un conjunto limitado de datos: solo 450 ejemplos. Para validación, usaremos los últimos 20,000 ejemplos del conjunto de entrenamiento original.
x_validation = x_train[40000:]
y_validation = y_train[40000:]
x_train = x_train[:450]
y_train = y_train[:450]
Esta es nuestra red:
model = keras.Sequential([
keras.layers.Flatten(input_shape=(28, 28)),
keras.layers.Dense(128, activation='relu'),
keras.layers.Dense(64, activation='relu'),
keras.layers.Dense(32, activation='relu'),
keras.layers.Dense(16, activation='relu'),
keras.layers.Dense(10)
])
model.compile(optimizer='rmsprop',
loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=True),
metrics=['accuracy'])
model.summary()
Output:
Model: "sequential"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
flatten (Flatten) (None, 784) 0
_________________________________________________________________
dense (Dense) (None, 128) 100480
_________________________________________________________________
dense_1 (Dense) (None, 64) 8256
_________________________________________________________________
dense_2 (Dense) (None, 32) 2080
_________________________________________________________________
dense_3 (Dense) (None, 16) 528
_________________________________________________________________
dense_4 (Dense) (None, 10) 170
=================================================================
Total params: 111,514
Trainable params: 111,514
Non-trainable params: 0
Ahora es momento de entrenarla. Aquí es donde usamos nuestros datos de validación, los alimentamos como una tupla en el argumento validation_data del método fit
history = model.fit(x_train, y_train, epochs=30, validation_data=(x_validation, y_validation), batch_size=15)
Ahora podemos ver si nuestra red sobreajusta. Para eso, verificaremos cómo cambia el valor de la loss después de cada epoch.
# Graficar valores de pérdida de entrenamiento y validación
plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
plt.title('Pérdida del modelo')
plt.ylabel('Pérdida')
plt.xlabel('Epoch')
plt.legend(['Entrenamiento', 'Validación'], loc='upper left')
plt.show()
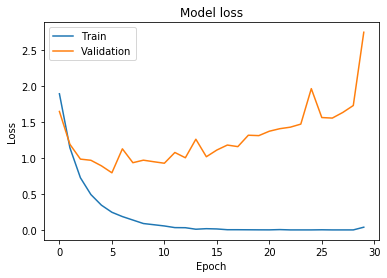
Después de cada ciclo de aprendizaje (epoch), nuestra red evalúa su rendimiento en los conjuntos de validación y entrenamiento. Idealmente, tanto la pérdida de entrenamiento como la de validación bajarían después de cada epoch, pero si la red sobreajusta, la pérdida de validación comenzará a subir.
Esto sucede cuando la red comienza a aprender peculiaridades en el conjunto de entrenamiento que realmente no representan patrones generales que se apliquen a datos no vistos. Esto causa que el rendimiento de la red baje mientras más la entrenamos.
Si prestas atención a nuestro gráfico puedes notar cómo la red comienza a sobreajustar alrededor de la 5ta epoch. Antes de estudiar soluciones evaluemos la red en nuestro conjunto de prueba.
test_loss, test_acc = model.evaluate(x_test, y_test, verbose=2)
print('Precisión de prueba:', test_acc)
print('Pérdida de prueba:', test_loss)
Output:
10000/10000 - 1s - loss: 2.8394 - accuracy: 0.7328
Precisión de prueba: 0.7328
Pérdida de prueba: 2.8394393890172243
Nuestra línea base es precisión de 0.73 y una pérdida de 2.83, veamos si podemos hacerlo mejor.
Primera solución: Parada temprana
La forma más simple de prevenir sobreajuste es detener el proceso de entrenamiento más temprano. Funciona porque las redes usualmente aprenden las características más amplias en el dataset antes de que comience a aprender el ruido.
En la práctica hacer esto es muy fácil. En nuestro ejemplo base ejecutamos 30 epochs, reduzcamos eso a 9 epochs y veamos si mejora las cosas.
history = model.fit(x_train, y_train, epochs=9, validation_data=(x_validation, y_validation), batch_size=15)
Ahora, grafiquemos los valores de pérdida:
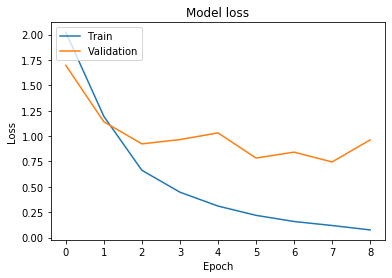
Puedes notar que en las últimas epochs la pérdida en el conjunto de validación comienza a subir, pero nunca crece tanto como en el caso base. También podemos verificar el rendimiento de la red en el conjunto de entrenamiento para ver si hubo una mejora.
test_loss, test_acc = model.evaluate(x_test, y_test, verbose=2)
print('Precisión de prueba:', test_acc)
print('Pérdida de prueba:', test_loss)
Output:
10000/10000 - 1s - loss: 0.9608 - accuracy: 0.7559
Precisión de prueba: 0.7559
Pérdida de prueba: 0.9607989938259125
Tuvimos una mejora modesta en precisión, de 0.73 a 0.75, y nuestra pérdida fue de 2.83 a 0.96, ¡nada mal si consideras que todo lo que hicimos fue reducir el número de epochs!
Probemos otra solución simple: reducir la complejidad de nuestra red.
Segunda solución: Reducir la complejidad de la red
Si nuestra red está aprendiendo demasiado ruido del conjunto de entrenamiento, intentar una red más pequeña podría ayudar. Una red más pequeña tiene un espacio de hipótesis más restringido, así que es más probable que se enfoque en aprender patrones generales y descuide peculiaridades en los datos.
En lugar de usar nuestra red base, probemos esta:
# Ahora construyamos el modelo
model = keras.Sequential([
keras.layers.Flatten(input_shape=(28, 28)),
keras.layers.Dense(32, activation='relu'),
keras.layers.Dense(10)
])
model.compile(optimizer='rmsprop',
loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=True),
metrics=['accuracy'])
model.summary()
Output:
Model: "sequential_2"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
flatten_2 (Flatten) (None, 784) 0
_________________________________________________________________
dense_10 (Dense) (None, 32) 25120
_________________________________________________________________
dense_11 (Dense) (None, 10) 330
=================================================================
Total params: 25,450
Trainable params: 25,450
Non-trainable params: 0
__________________________
Nuestros parámetros entrenables ahora son solo 25,450, abajo de los 111,514 originales. La entrenaremos por 30 epochs como en el caso base.
history = model.fit(x_train, y_train, epochs=30, validation_data=(x_validation, y_validation), batch_size=15)
Y, como en el caso anterior, graficar la pérdida y evaluar el rendimiento en el conjunto de entrenamiento.
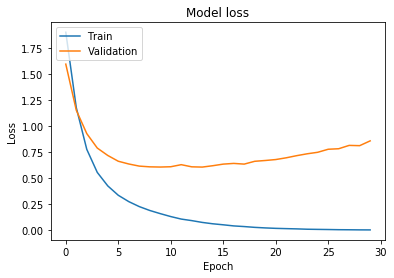
test_loss, test_acc = model.evaluate(x_test, y_test, verbose=2)
print('Precisión de prueba:', test_acc)
print('Pérdida de prueba:', test_loss)
Output:
10000/10000 - 0s - loss: 0.8094 - accuracy: 0.8216
Precisión de prueba: 0.8216
Pérdida de prueba: 0.8094104566439986
Puedes notar que la pérdida ahora está subiendo de una forma mucho más suave, nuestra precisión mejoró y nuestra pérdida disminuyó. Otra vez, resultados bastante buenos por hacer menos trabajo que en nuestro caso base.
Tercera solución: Usar dropout
La última técnica que usaremos es tal vez la más elaborada: el uso de capas dropout en nuestra red.
Las capas dropout ‘apagan’ un porcentaje de los nodos durante el entrenamiento. Esto significa que solo entrenarás subsecciones aleatorizadas de la red en cada actualización de peso.
¿Por qué funciona esto? El principio es muy similar a lo que pasa con los modelos de ensamble: entrenas diferentes modelos y usas un resultado agregado de ellos para producir predicciones. Los errores de todos los modelos se cancelan entre sí y al final, obtienes mejores resultados.
Al entrenar independientemente subsecciones de la red terminamos con un modelo final que es menos propenso al sobreajuste y generaliza mejor. ¿Cómo implementas esto en Keras? Hay una capa especial llamada Dropout que recibe como parámetro el porcentaje de pesos que debe apagar.
Construyamos una red que use 3 capas Dropout encima de nuestro modelo base:
model = keras.Sequential([
keras.layers.Flatten(input_shape=(28, 28)),
keras.layers.Dropout(0.2),
keras.layers.Dense(128, activation='relu'),
keras.layers.Dense(64, activation='relu'),
keras.layers.Dropout(0.2),
keras.layers.Dense(32, activation='relu'),
keras.layers.Dense(16, activation='relu'),
keras.layers.Dropout(0.5),
keras.layers.Dense(10)
])
model.compile(optimizer='rmsprop',
loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=True),
metrics=['accuracy'])
Output:
model.summary()
Model: "sequential_3"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
flatten_3 (Flatten) (None, 784) 0
_________________________________________________________________
dropout (Dropout) (None, 784) 0
_________________________________________________________________
dense_12 (Dense) (None, 128) 100480
_________________________________________________________________
dense_13 (Dense) (None, 64) 8256
_________________________________________________________________
dropout_1 (Dropout) (None, 64) 0
_________________________________________________________________
dense_14 (Dense) (None, 32) 2080
_________________________________________________________________
dense_15 (Dense) (None, 16) 528
_________________________________________________________________
dropout_2 (Dropout) (None, 16) 0
_________________________________________________________________
dense_16 (Dense) (None, 10) 170
=================================================================
Total params: 111,514
Trainable params: 111,514
Non-trainable params: 0
Y entrenarla por 30 epochs
history = model.fit(x_train, y_train, epochs=30, validation_data=(x_validation, y_validation), batch_size=15)
Estos son los resultados:
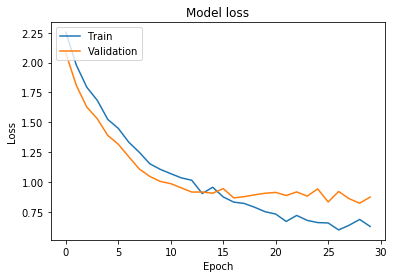
test_loss, test_acc = model.evaluate(x_test, y_test, verbose=2)
print('Precisión de prueba:', test_acc)
print('Pérdida de prueba:', test_loss)
Output:
10000/10000 - 1s - loss: 0.8912 - accuracy: 0.8258
Precisión de prueba: 0.8258
Pérdida de prueba: 0.891159076166153
¡Genial! Obtuvimos mejores resultados que en nuestro caso base, y la curva de pérdida nos hace preguntarnos si la red aún puede ser entrenada por más epochs antes de que sobreajuste.
Usar Dropout es un método muy popular con redes neuronales convolucionales y procesamiento de imágenes con RNs. Si estás interesado en estos temas estar familiarizado con dropout te será útil.
¿Eso es todo?
Nop, ¿por qué no experimentas un poco? Toma el código de este artículo e intenta lo siguiente:
- Entrena la red por menos de 9 epochs. ¿Cuáles son los resultados si la entrenas por 5 epochs? ¿Qué tal 3?
- Prueba una red más pequeña, o prueba diferentes números de capas y tamaños y compara los resultados.
- Usa capas dropout con diferentes porcentajes, prueba 0.1, o 0.3. Ponlas en diferentes lugares y ve cómo afecta los resultados.
- Prueba diferentes combinaciones de todos estos enfoques, ¡diviértete!
La regularización es un tema muy importante, central para soluciones profesionales que usan redes neuronales. Como la mayoría de cosas en este campo es una parte ciencia y una parte arte, así que sigue ejecutando experimentos hasta que le agarres la onda.
El siguiente artículo será el último en esta serie. Discutiremos algunas consideraciones finales y ofreceremos algunos consejos para continuar aprendiendo sobre este tema fascinante.
¡Gracias por leer!
Qué hacer después
- Comparte este artículo con amigos y colegas. Gracias por ayudarme a llegar a personas que podrían encontrar esta información útil.
- Aquí está la documentación oficial de Keras
- Puedes encontrar el código fuente para esta serie aquí
- Este artículo está basado en el libro: Grokking Deep Learning y en Deep Learning (Goodfellow, Bengio, Courville).
- Envíame un email con preguntas, comentarios o sugerencias (está en la página Autor)
