Ya cubrimos los conceptos más importantes de deep learning y creamos diferentes implementaciones usando Python vanilla. Ahora, estamos en una posición donde podemos empezar a construir algo un poco más elaborado.
Usaremos un enfoque más práctico construyendo un modelo de deep learning para clasificación usando software de categoría profesional.
Aprenderás cómo hacer un clasificador para dígitos escritos a mano usando Keras, ejecutándose sobre Tensorflow.
¡Genial, empecemos!
Antes de proceder, ¿qué es Keras?
Keras es una biblioteca popular para crear modelos de deep learning.
Es una API de alto nivel que ejecuta sobre múltiples backends que manejan todo el procesamiento, como Tensorflow, Theano o Microsoft Cognitive Toolkit.
Desde que se lanzó Tensorflow 2, Keras se convirtió en su API oficial de alto nivel, así que ahora viene incluido por defecto con la instalación de Tensorflow.
Configuración
En lugar de escribir instrucciones que podrían quedar desactualizadas, solo enlazaré a los recursos oficiales. Necesitarás instalar estos:
¡Bien, empecemos!
Importar las bibliotecas y obtener los datos
Podemos obtener todas las bibliotecas que necesitamos con las siguientes líneas:
# Importar TensorFlow y Keras
import TensorFlow as tf
from tensorflow import keras
# Importar bibliotecas de apoyo para gráficos
import matplotlib.pyplot as plt
Ahora, obtengamos los datos. Usaremos el conjunto MNIST de dígitos escritos a mano, uno de los datasets más populares para probar modelos de clasificación de imágenes ML. El conjunto incluye 60,000 ejemplos para entrenamiento y 10,000 para pruebas:
(x_train, y_train), (x_test, y_test) = mnist.load_data()
El método load_data devuelve dos tuplas:
- (x_train, y_train) son los 60,000 ejemplos que usaremos para entrenar la red.
- (x_test, y_test) son los ejemplos que usaremos para evaluar el rendimiento de la red.
Explorar los datos
x_train.shape
Output: (60000, 28, 28)
y_train.shape
Output: (60000,)
x_train es una colección de 60,000 matrices de 28x28, donde cada entrada en la matriz es un número de 0 a 255. Cada matriz de 28x28 representa un número escrito a mano, píxel por píxel. Puedes visualizarlos usando PyPlot.
# Imprimir el primer elemento en x_train como una imagen
plt.figure()
plt.imshow(x_train[0])
plt.colorbar()
plt.grid(False)
plt.show()
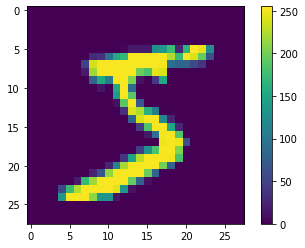
y_train es una colección de 60,000 etiquetas, en este caso representando el número que representa su respectivo elemento de x_train. Si recuerdas artículos anteriores, estos son los valores esperados.
Verifiquemos que la etiqueta para el primer elemento es un cinco:
y_train[0]
Output: 5
Preprocesamiento de los datos
No se necesita mucho para este dataset particular. Las redes neuronales funcionan mejor si sus entradas están entre 0 y 1, así que realicemos algo de normalización en las entradas:
x_train = x_train / 255.0
x_test = x_test / 255.0
Estas dos líneas hicieron el truco, ahora podemos empezar a construir nuestra red.
Construir la red
Ahora construiremos y compilaremos nuestra red neuronal. En Keras, solo necesitas definir las capas en tu red y casi has terminado. Esta es la red de 8 capas que usaremos:
model = keras.Sequential([
keras.layers.Flatten(input_shape=(28, 28)),
keras.layers.Dense(512, activation='relu'),
keras.layers.Dense(216, activation='relu'),
keras.layers.Dense(128, activation='relu'),
keras.layers.Dense(64, activation='relu'),
keras.layers.Dense(32, activation='relu'),
keras.layers.Dense(16, activation='relu'),
keras.layers.Dense(10, activation='softmax')
])
Keras tiene muchos tipos diferentes de capas, nuestra red está hecha de dos tipos principales: 1 capa Flatten y 7 capas Dense.
Una capa Flatten se usa para transformar tensores de dimensiones más altas en vectores. En nuestro caso, transforma una matriz de 28x28 en un vector con 728 entradas (28x28=784).
Las capas Dense necesitan que especifiques la forma de la salida (el primer parámetro) y la función de activación. Todas nuestras capas tienen activación relu excepto la última capa. La capa de salida usa softmax porque esa es la elección correcta cuando construyes un clasificador multiclase.
El siguiente paso es compilar el modelo:
model.compile(loss='sparse_categorical_crossentropy',
optimizer='adam',
metrics=['accuracy'])
Estos parámetros son:
- loss: Es la función de puntuación de optimización, el número que la red tratará de reducir durante el entrenamiento.
- optimizer: Es el algoritmo usado para actualizar los valores de los pesos en la red.
- metrics: Mediciones que realizamos durante el entrenamiento.
Puedes verificar la forma final de la red usando el método .summary():
model.summary()
Output:
Model: "sequential"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
flatten (Flatten) (None, 784) 0
_________________________________________________________________
dense (Dense) (None, 512) 401920
_________________________________________________________________
dense_1 (Dense) (None, 216) 110808
_________________________________________________________________
dense_2 (Dense) (None, 128) 27776
_________________________________________________________________
dense_3 (Dense) (None, 64) 8256
_________________________________________________________________
dense_4 (Dense) (None, 32) 2080
_________________________________________________________________
dense_5 (Dense) (None, 16) 528
_________________________________________________________________
dense_6 (Dense) (None, 10) 170
=================================================================
Total params: 551,538
Trainable params: 551,538
Non-trainable params: 0
¿Por qué usamos una red con esta forma? Bueno, para ser honesto, porque se me ocurrió construir una con 9 capas. Puedes intentar construir una red más pequeña como ejercicio y ver cómo cambia el rendimiento:
model = keras.Sequential([
keras.layers.Flatten(input_shape=(28, 28)),
keras.layers.Dense(216, activation='relu'),
keras.layers.Dense(10, activation='softmax')
Entrenar la red y evaluar su precisión
Entrenamos la red usando el método fit():
history = model.fit(x_train, y_train, epochs=20, batch_size=15)
Los primeros dos argumentos son los ejemplos de entrenamiento y sus etiquetas, y el tercer argumento es el número de ciclos de entrenamiento que ejecutaremos (en este caso 20). batch_size te dice el número de muestras que serán propagadas a través de la red antes de actualizar los pesos. En nuestra red actualizaremos pesos cada vez que procesemos 15 entradas.
Fit devuelve un objeto history con información sobre el proceso de entrenamiento. Cuando llames al método fit verás la siguiente salida:
Train on 60000 samples
Epoch 1/20
60000/60000 [==============================] - 25s 420us/sample - loss: 0.2670 - accuracy: 0.9205
Epoch 2/20
60000/60000 [==============================] - 25s 412us/sample - loss: 0.1127 - accuracy: 0.9670
Epoch 3/20
60000/60000 [==============================] - 26s 440us/sample - loss: 0.0833 - accuracy: 0.9768
Epoch 4/20
60000/60000 [==============================] - 24s 400us/sample - loss: 0.0668 - accuracy: 0.9816
Epoch 5/20
60000/60000 [==============================] - 25s 418us/sample - loss: 0.0579 - accuracy: 0.9838
Epoch 6/20
60000/60000 [==============================] - 36s 606us/sample - loss: 0.0475 - accuracy: 0.9871
Epoch 7/20
60000/60000 [==============================] - 36s 598us/sample - loss: 0.0421 - accuracy: 0.9887
Epoch 8/20
60000/60000 [==============================] - 35s 580us/sample - loss: 0.0356 - accuracy: 0.9905
Epoch 9/20
60000/60000 [==============================] - 32s 534us/sample - loss: 0.0341 - accuracy: 0.9911
Epoch 10/20
60000/60000 [==============================] - 28s 461us/sample - loss: 0.0296 - accuracy: 0.9925
Epoch 11/20
60000/60000 [==============================] - 28s 463us/sample - loss: 0.0289 - accuracy: 0.9927
Epoch 12/20
60000/60000 [==============================] - 28s 459us/sample - loss: 0.0284 - accuracy: 0.9936
Epoch 13/20
60000/60000 [==============================] - 28s 467us/sample - loss: 0.0259 - accuracy: 0.9938
Epoch 14/20
60000/60000 [==============================] - 27s 455us/sample - loss: 0.0259 - accuracy: 0.9938
Epoch 15/20
60000/60000 [==============================] - 29s 486us/sample - loss: 0.0206 - accuracy: 0.9952
Epoch 16/20
60000/60000 [==============================] - 28s 471us/sample - loss: 0.0241 - accuracy: 0.9945
Epoch 17/20
60000/60000 [==============================] - 28s 469us/sample - loss: 0.0211 - accuracy: 0.9952
Epoch 18/20
60000/60000 [==============================] - 28s 461us/sample - loss: 0.0172 - accuracy: 0.9960
Epoch 19/20
60000/60000 [==============================] - 25s 424us/sample - loss: 0.0209 - accuracy: 0.9953
Epoch 20/20
60000/60000 [==============================] - 31s 510us/sample - loss: 0.0170 - accuracy: 0.9959
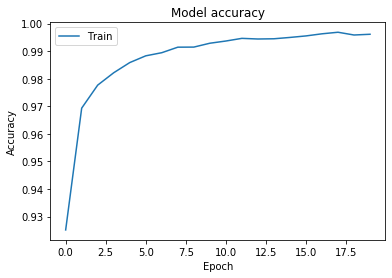
Te dice epoch por epoch cómo cambian los valores de pérdida y precisión. Como se esperaba, cada epoch los resultados se vuelven un poco mejores. Si prefieres, puedes graficarlos usando PyPlot.
# Graficar valores de precisión de entrenamiento y validación
plt.plot(history.history['accuracy'])
plt.title('Precisión del modelo')
plt.ylabel('Precisión')
plt.xlabel('Epoch')
plt.legend(['Entrenamiento'], loc='upper left')
plt.show()
# Graficar valores de pérdida de entrenamiento y validación
plt.plot(history.history['loss'])
plt.title('Pérdida del modelo')
plt.ylabel('Pérdida')
plt.xlabel('Epoch')
plt.legend(['Entrenamiento'], loc='upper left')
plt.show()
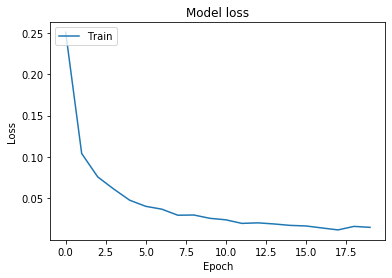
Entonces, obtenemos una precisión final de 99.61, pero también podrías recordar que evaluar rendimiento en el conjunto de entrenamiento no tiene mucho sentido, así que probemos el modelo en datos que no ha visto aún.
test_loss, test_acc = model.evaluate(x_test, y_test, verbose=0)
print('Precisión de prueba:', test_acc)
print('Pérdida de prueba:', test_loss)
Output:
Precisión de prueba: 0.9822
Pérdida de prueba: 0.14858887433931195
¡Genial! ¡Precisión de 98.61% con una pérdida de 0.01, nada mal para nuestro primer intento en este dataset!
Hay muchas formas de mejorar estos resultados, pero por ahora, es suficiente estar contentos con nuestro arduo trabajo.
Mientras nos acercamos más a ejemplos del mundo real con redes neuronales, nos acercamos más al final de esta serie. En el siguiente artículo, hablaremos sobre regularización: una serie de técnicas que podemos usar para luchar contra el sobreajuste en nuestros modelos de DL.
¡Gracias por leer!
Qué hacer después
- Comparte este artículo con amigos y colegas. Gracias por ayudarme a llegar a personas que podrían encontrar esta información útil.
- Prueba diferentes redes, tanto más grandes como más pequeñas, y ve cómo el tamaño de la red afecta el rendimiento tanto en los conjuntos de entrenamiento como de prueba. También puedes intentar entrenar una cantidad diferente de epochs.
- Aquí está la documentación oficial de Keras
- Puedes encontrar el código fuente para esta serie aquí
- Este artículo está basado en el libro: Grokking Deep Learning y en Deep Learning (Goodfellow, Bengio, Courville).
- Envíame un email con preguntas, comentarios o sugerencias (está en la página Autor)
