Fundamentos de Deep Learning (7): Correlación

En artículos anteriores, aprendimos cómo las redes neuronales ajustan sus pesos para mejorar la precisión de sus predicciones usando técnicas como el descenso de gradiente.

En este artículo, echaremos un vistazo al proceso de aprendizaje usando una perspectiva más abstracta. Discutiremos la correlación entre entradas y salidas en un conjunto de entrenamiento, y cómo las redes neuronales encuentran patrones en los datos.

Hola, mi nombre es Conejillo de Indias

Usaremos un experimento hipotético como trasfondo para aprender sobre correlación. Supón que formas parte de un experimento cuyo objetivo es… bueno, no se me ocurre ninguna razón más que torturarte. El experimento es bastante simple:

Frente a ti, hay tres botones (rojo, verde y azul) y una palanca. Te piden que presiones cualquier configuración de botones y luego jales la palanca. Para algunas configuraciones, recibes una descarga eléctrica, y para otras recibes dulces. Te piden que encuentres un patrón por prueba y error.

Después de jugar con el sistema por un rato (y sufrir varias descargas eléctricas), escribes el siguiente patrón:

Cada fila en la imagen representa una combinación de botones y su respectivo resultado. En la primera fila, por ejemplo, solo se presionó el botón azul y recibiste una descarga eléctrica. En la tercera fila, presionaste todos los botones y recibiste dulces en su lugar.

Queremos entrenar una red neuronal para jugar este juego. Cuando se le dé información sobre qué botones fueron presionados, predecirá el resultado, ya sean dulces o descarga eléctrica.

Enviando patrones

Nuestra red neuronal realizará una acción muy simple: mapeará un patrón de entradas a salidas. En el fondo, esto es lo que hacen las redes neuronales: mapear un conjunto de entradas a un conjunto de salidas.

Tenemos un conjunto de datos completo para entrenar nuestra red, pero las redes no entienden colores de botones o la diferencia entre ser electrocutado o tener dulces. Necesitamos transformar nuestros datos de entrenamiento a una forma que nuestra red pueda entender.

La forma más común de hacer esto es creando una matriz que represente el mismo patrón, como esta:

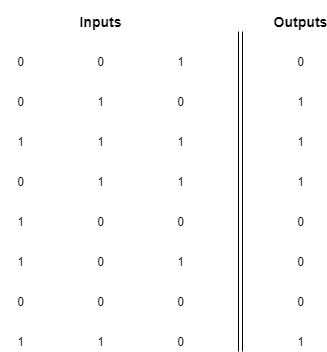
En nuestra representación matricial para las entradas, el valor 1 significa que el botón fue presionado y 0 significa que no fue presionado. La primera columna representa el botón rojo, la columna del medio representa el verde y la columna derecha el azul.

En nuestra columna de salidas, representamos la descarga eléctrica con un 0 y los dulces con un 1.

Hay otras formas de representar este patrón, podrías, por ejemplo, escribir la siguiente matriz:

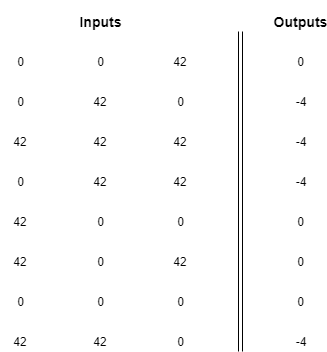
Existe un número infinito de matrices que codifican este mismo patrón, lo cual nos lleva a tener una idea muy importante: las redes neuronales no entienden los datos que se les envían, solo encuentran un mapeo entre el patrón en las entradas y el patrón en las salidas.

Depende del ser humano que usa la red descubrir el significado de los resultados. Mientras encuentres una forma consistente de representar entradas y salidas, la red hará su mejor esfuerzo para encontrar un mapeo.

Aprendiendo correlación por atribución de errores

El siguiente paso es entender cómo las redes neuronales aprenden la correlación.

El título medio que lo dice: una red neuronal calcula un error y luego actualiza pesos para reducir el error a 0. Estudiamos en artículos anteriores cómo usar el descenso de gradiente para actualizar el valor de los pesos en la dirección correcta (subir o bajar su valor).

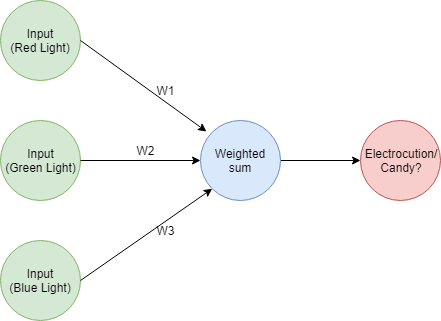
Recuerda que una red neuronal realiza una suma ponderada usando los vectores de entrada y peso. Después de calcular el error procede a actualizar los pesos con la esperanza de reducir el valor del error. En este paso de actualización, pueden suceder 3 cosas:

• Los pesos que multiplicaron entradas con una correlación positiva con la salida aumentan en valor. Esta es una forma de darle más importancia a esas entradas y permitirles jalar la predicción en la dirección del valor esperado.
• Los pesos que multiplicaron entradas con una correlación negativa con la salida disminuyen en valor. Esta es una forma de proteger la predicción de ser influenciada por las entradas que la jalan lejos del valor esperado.
• Si el peso multiplicó una entrada con un valor de 0, no pasa nada. Tales entradas no pudieron haber afectado la predicción, así que no se necesita actualización en los pesos.

Aparte de la dirección de la actualización, hay otro mecanismo importante para atribuir error a una entrada particular. Recuerda que el factor de actualización de peso se calcula como alpha * input * (predicted_value - expected_value), nota que toda la expresión se multiplica por input.

Si el valor de la entrada es alto y el error también es alto, podemos asumir que la contribución individual de esa entrada al error fue grande, y actualizar en consecuencia. Por otro lado, si la entrada tuvo un valor de 0, sabemos que esa entrada particular no contribuyó nada al error.

Podemos realizar un análisis informal con las entradas y salidas y entender la dirección en la que se actualizan los pesos. Veamos nuestro primer ejemplo, correspondiente a la 4ta fila en la matriz. En este caso, tenemos:

• Luz roja estaba apagada (0)
• Luz verde estaba encendida (1)
• Luz azul estaba encendida (1)
• Obtuvimos dulces (1)

Sabemos que la luz roja no contribuyó nada al error, así que su peso asociado no necesita cambiar. La luz verde y azul, por otro lado, ambas contribuyeron al resultado y tienen una correlación positiva con él (1). Debido a esto, sabemos que el valor de sus pesos asociados debería ser empujado hacia arriba.

Ahora revisemos la fila número seis, donde obtuvimos:

• Luz roja estaba encendida (1)
• Luz verde estaba apagada (0)
• Luz azul estaba encendida (1)
• Obtuvimos una descarga eléctrica (0)

Sabemos que la luz verde no contribuyó nada porque era un 0, así que no hay cambio en su peso. Pero ahora, tanto la luz roja como la azul contribuyeron al resultado de 0 con una correlación negativa. En este escenario, los pesos asociados con el rojo y azul deberían ser empujados hacia abajo.

Puedes crear una matriz adicional mostrando la tendencia a aumentar o disminuir los pesos:

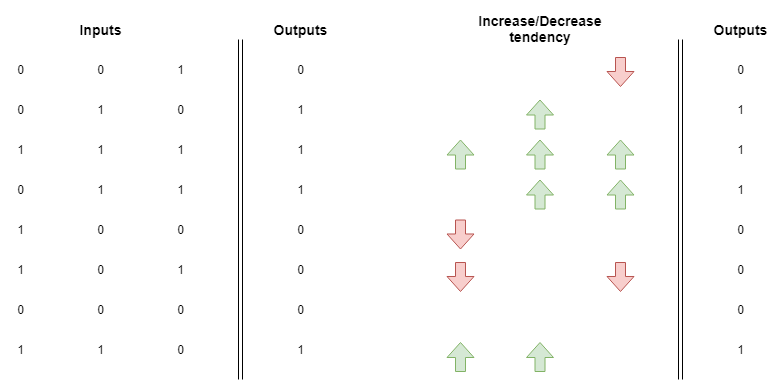
Si promedias estos notarás que el peso para la entrada verde tiene una tendencia a subir. Esto significa que después de entrenar una red neuronal con todos estos ejemplos, la luz verde tendrá un peso con un valor más alto que las luces roja y azul.

Lo que esto significa es que hay una alta correlación positiva entre presionar la luz verde y obtener dulces

Esta representación sobre-simplificada te permite olvidarte de las complejidades del descenso de gradiente y solo concentrarte en un hecho simple: el aprendizaje recompensa las entradas que están correlacionadas con salidas específicas asignándoles pesos más grandes.

Este ejemplo es un poco diferente de los anteriores respecto al tamaño del conjunto de entrenamiento. En artículos anteriores, teníamos solo un ejemplo para el que optimizamos, mientras que ahora tenemos 8 de ellos. Aprendamos cómo usar el descenso de gradiente para entrenar una red neuronal con más de un elemento en el conjunto de entrenamiento.

Descenso de gradiente estocástico

Descenso de gradiente estocástico es solo un término elegante que significa ejecutar descenso de gradiente para cada ejemplo en el conjunto de entrenamiento y actualizar pesos en consecuencia.

Funciona así:

1. Toma el primer ejemplo en el conjunto de entrenamiento.
2. Haz una predicción, calcula el error y actualiza los pesos
3. Realiza (1) y (2) otra vez con el segundo elemento en el conjunto de entrenamiento, luego el tercero, y así sucesivamente. Ejecuta este ciclo hasta que la red prediga las salidas lo suficientemente bien para cada entrada.

En los artículos anteriores, implementamos todas nuestras redes desde cero usando solo las características estándar de Python.

Ahora implementaremos nuestra red usando una biblioteca popular llamada NumPy. Manejará operaciones de matrices y vectores por nosotros resultando en una implementación más concisa.

Primero, configuremos las variables. Todos los vectores y matrices serán arrays de NumPy:

import numpy as nmpy

# Configuración de variables: usamos el array de NumPy para crear una implementación más concisa
alpha = 0.1
weights = nmpy.array([0.5, 0.5, 0.5])

# Las entradas y resultados esperados están en orden correspondiente
inputs = nmpy.array([[0,0,1],
 [0,1,0],
 [1,1,1],
 [0,1,1],
 [1,0,0],
 [1,0,1],
 [0,0,0],
 [1,1,0]
 ])

expected_values = nmpy.array([0,1,1,1,0,0,0,1])

Ahora, implementemos el bucle de ajuste de pesos.

Porque estamos realizando la versión estocástica del descenso de gradiente, realizaremos ejecuciones que entrenen la red con cada elemento en el conjunto de entrenamiento. En este caso, ejecutaremos el ciclo 15 veces.

La implementación será mucho más concisa que en ejemplos anteriores porque NumPy manejará todas las operaciones de vector/matriz por nosotros.

# Ejecutemos la optimización para cada entrada 15 veces
for run in range(15):
 # Este es el error total de una sola ejecución
 error_for_run = 0
 # Ahora aplicamos descenso de gradiente a cada par de entradas/valores esperados
 for input_set, expected_value in zip(inputs, expected_values):

 # Podemos calcular nuestro valor predicho con una simple operación de producto punto, ¡genial!
 predicted_value = round( input_set.dot(weights), 1)
 print("Nuestra red predijo {} para las entradas {}".format(predicted_value, input_set))

 # El cálculo de error es el mismo que antes, ¡pero con la magia de NumPy!
 error = (predicted_value - expected_value) ** 2
 error_for_run += error

 # Con la magia de NumPy, ¡actualizar pesos es así de fácil!
 weights -= alpha * (input_set * (predicted_value - expected_value) )

 print("El error acumulado para esta ejecución es {} \n\n\n".format(error_for_run))

Nota lo siguiente:

• Mantenemos el error general para cada ejecución individual, cuyo valor es la suma de los errores en la predicción de cada elemento en el conjunto.
• El valor predicho es solo un producto punto entre las entradas y los pesos. Redondeamos a 1 decimal por conveniencia.
• El cálculo de error y las actualizaciones de peso usan los operadores sobrecargados de NumPy para suma, resta y multiplicación. ¿Recuerdas cuánto código requería en artículos anteriores? Ese es el poder de usar bibliotecas especialmente diseñadas para estas tareas.

Puedes verificar que este código realiza el ajuste de peso correcto ejecutándolo e inspeccionando los resultados:

Nuestra red predijo 0.5 para las entradas [0 0 1]
Nuestra red predijo 0.5 para las entradas [0 1 0]
Nuestra red predijo 1.5 para las entradas [1 1 1]
Nuestra red predijo 0.9 para las entradas [0 1 1]
Nuestra red predijo 0.4 para las entradas [1 0 0]
Nuestra red predijo 0.8 para las entradas [1 0 1]
Nuestra red predijo 0.0 para las entradas [0 0 0]
Nuestra red predijo 0.8 para las entradas [1 1 0]
El error acumulado para esta ejecución es 1.6



Nuestra red predijo 0.3 para las entradas [0 0 1]
Nuestra red predijo 0.5 para las entradas [0 1 0]
Nuestra red predijo 1.2 para las entradas [1 1 1]
Nuestra red predijo 0.8 para las entradas [0 1 1]
Nuestra red predijo 0.3 para las entradas [1 0 0]
Nuestra red predijo 0.6 para las entradas [1 0 1]
Nuestra red predijo 0.0 para las entradas [0 0 0]
Nuestra red predijo 0.8 para las entradas [1 1 0]
El error acumulado para esta ejecución es 0.9099999999999999

... más iteraciones ...

Nuestra red predijo 0.0 para las entradas [0 0 1]
Nuestra red predijo 0.9 para las entradas [0 1 0]
Nuestra red predijo 1.0 para las entradas [1 1 1]
Nuestra red predijo 1.0 para las entradas [0 1 1]
Nuestra red predijo 0.0 para las entradas [1 0 0]
Nuestra red predijo 0.0 para las entradas [1 0 1]
Nuestra red predijo 0.0 para las entradas [0 0 0]
Nuestra red predijo 1.0 para las entradas [1 1 0]
El error acumulado para esta ejecución es 0.009999999999999995



Nuestra red predijo 0.0 para las entradas [0 0 1]
Nuestra red predijo 1.0 para las entradas [0 1 0]
Nuestra red predijo 1.0 para las entradas [1 1 1]
Nuestra red predijo 1.0 para las entradas [0 1 1]
Nuestra red predijo 0.0 para las entradas [1 0 0]
Nuestra red predijo 0.0 para las entradas [1 0 1]
Nuestra red predijo 0.0 para las entradas [0 0 0]
Nuestra red predijo 1.0 para las entradas [1 1 0]
El error acumulado para esta ejecución es 0.0

¡Genial, ahora sabemos cómo implementar descenso de gradiente estocástico!

A veces una capa no es suficiente

Tuvimos suerte con nuestro conjunto de entrenamiento porque había una correlación clara entre entradas y salidas.

El botón verde tenía una correlación muy fuerte con el resultado de dulces. Los botones rojo y azul no tenían una tendencia clara, así que la red tuvo que esperar hasta que el peso de la luz verde convergiera a un valor para corregir los pesos de estos otros dos botones. Cuando la luz verde estaba generando los resultados correctos, tanto la luz roja como la azul absorbieron todo el error en la predicción, y la corrección fue posible.

A veces el conjunto de entrenamiento no tiene patrones tan claros. ¿Qué pasa si por ejemplo todos tienen la misma tendencia a subir y bajar? En este escenario, es posible construir capas intermedias en la red que realmente tengan una correlación con la salida.

Esta es la base del deep learning: redes neuronales multi-capa. Construir redes con muchas capas te permitirá resolver problemas que redes más pequeñas no pueden resolver. Por supuesto, esto viene con desafíos: ¿cómo atribuyes error a capas en las primeras etapas de la predicción?

Esto tiene una solución: retropropagación. En el siguiente artículo, aprenderemos cómo las redes neuronales con muchas capas usan esta técnica para actualizar correctamente los pesos a través de toda la red.

Qué hacer después

• Comparte este artículo con amigos y colegas. Gracias por ayudarme a llegar a personas que podrían encontrar esta información útil.
• Este artículo está basado en el libro: Grokking Deep Learning y en Deep Learning (Goodfellow, Bengio, Courville).
• Puedes encontrar el código fuente para esta serie aquí
• Envíame un email con preguntas, comentarios o sugerencias (está en la página Autor)