En el artículo anterior aprendimos que las redes neuronales buscan la correlación entre las entradas y las salidas de un conjunto de entrenamiento. También aprendimos que basándose en el patrón, los pesos tendrán una tendencia general a aumentar o disminuir hasta que la red prediga todos los valores correctamente.
A veces no hay una dirección clara en esta tendencia arriba/abajo y la red tendrá problemas aprendiendo un patrón. En el siguiente ejemplo, cada peso es jalado hacia arriba con la misma fuerza con que es jalado hacia abajo.
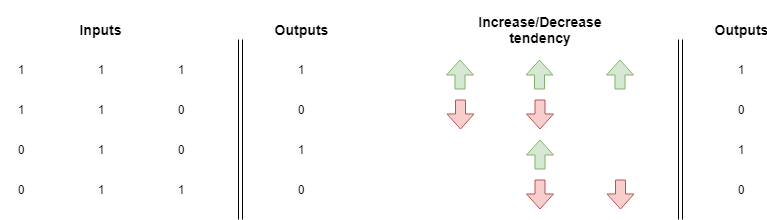
Puedes hacer la prueba tomando nuestra implementación del descenso de gradiente y reemplazando la sección de configuración de datos con esta:
# Las entradas y resultados esperados están en orden correspondiente
inputs = nmpy.array([[1,1,1],
[1,1,0],
[0,1,0],
[0,1,1]
])
expected_values = nmpy.array([1,0,1,0])
Puedes ejecutarlo y verificar que nunca converge. Incluso podrías aumentar el número de iteraciones, pero no ayudará: la red no puede encontrar una correlación apropiada entre entradas y salidas.
Este problema es bastante común, y como imaginaste, la gente ya encontró una solución. Si la red no puede encontrar una correlación clara entre entradas y salidas, aún podemos crear un conjunto intermedio que tenga una correlación real con las salidas.
Este conjunto será calculado usando las entradas. En el mundo de las redes neuronales, podemos hacer esto creando cualquier número de capas intermedias.
Visualizando redes neuronales multi-capa
Entonces, recordemos cómo se ve nuestra red
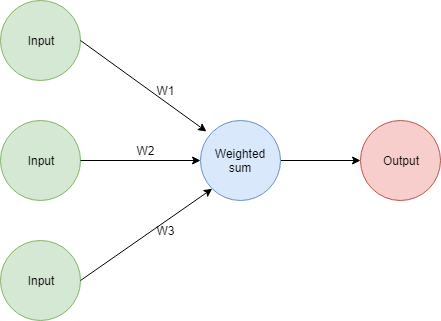
Podemos crear una capa adicional en la red con cualquier número de nodos. La misma red con una capa adicional de 4 nodos se vería así:
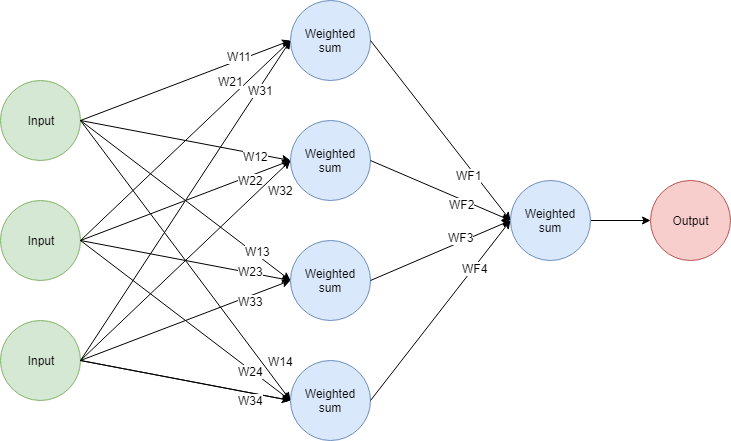
Funciona así:
- Cada nodo en la segunda capa realiza una suma ponderada de las entradas. Esto significa que hay 12 nuevos pesos usados para producir las entradas de la capa media.
- Las salidas de los 4 nodos en la capa media funcionan como entradas para la capa final. La capa final realiza una suma ponderada (así que se usan 4 pesos ahí) y produce una salida.
Puedes ver esto como dos redes apiladas juntas. Las salidas de la primera parte de la red son las entradas para la segunda parte. Estas capas adicionales usualmente se llaman las capas ocultas de la red.
Bien, ahora entiendes cómo la red realiza predicciones, pero ¿cómo podemos ajustar los pesos? Para esto, necesitamos entender una nueva técnica: retropropagación.
Retropropagación: atribución de errores a través de capas
Recordemos una lección importante de artículos anteriores: los pesos se actualizan basándose en su contribución al error en una predicción. Las redes neuronales cambian el valor de sus pesos en un intento de reducir sus errores.
Esta es también la razón por la que multiplicamos por el valor de la entrada respectiva cuando calculamos el factor de corrección para un peso. Si la entrada tuvo un valor de 0, puedes estar seguro de que el peso por el que fue multiplicada no contribuyó en absoluto al error general en la predicción.
Este cálculo era bastante directo porque podías asociar directamente entradas y pesos al error general: tenías una capa y un producto punto, así que el cálculo era directo. Pero ¿cómo podemos hacer eso cuando tenemos múltiples capas? ¿Cómo podemos corregir los valores de pesos al principio de la red?
Para eso, necesitamos poder calcular la contribución de error de cada peso en la red. El truco está en entender cómo la nueva capa y sus pesos (WF*) contribuyen al error final.
Mira esta red con valores ficticios:
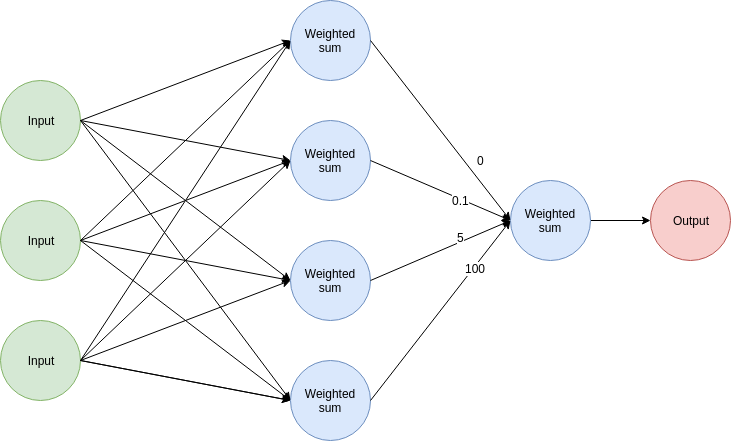
Puedes hacer las siguientes suposiciones sobre una predicción:
- El nodo superior no contribuyó al error general porque su peso asociado tiene un valor de 0. No importa qué valor tuvo el nodo como salida, multiplicarlo por 0 asegura que no contribuyó nada al resultado final.
- El nodo inferior tuvo una contribución mucho mayor que los otros nodos debido al alto valor (100) de su peso asociado comparado con los otros.
Entonces, da un paso atrás y míralo desde este ángulo: podemos usar los valores de los pesos en esa capa como una medida de cuánto contribuyó cada nodo al error general.
Podemos usar esta idea para calcular los factores de corrección para las capas anteriores así:
- Calculamos el valor de un delta, que usamos en nuestros artículos anteriores para calcular los factores de ajuste de peso. Este es otro nombre para el factor (predicted_value - expected_value). En este caso, tiene un valor de 2.
- Multiplicamos el valor de delta por los valores de los pesos de la segunda capa. Estos valores se usarán para calcular los factores de ajuste de peso para la capa anterior usando la misma ecuación de corrección de peso con la que hemos estado trabajando.
Otra vez, esto es más fácil de visualizar con una imagen:
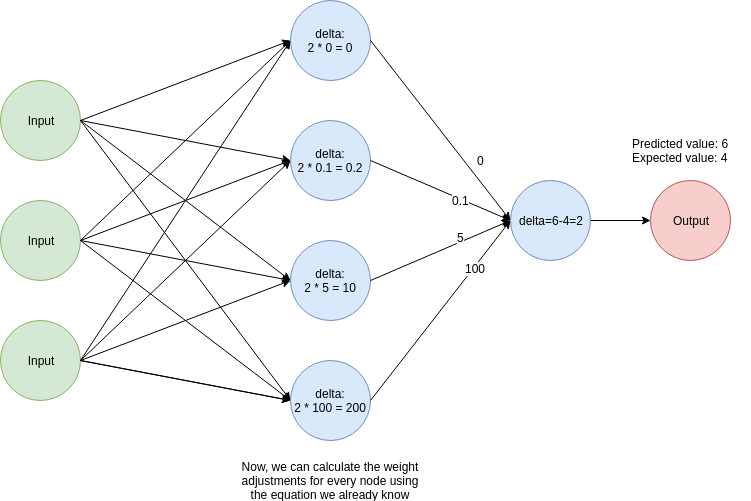
¡Genial! Estamos casi listos para implementar retropropagación en Python. Antes de escribir el código completo, tengamos una breve discusión sobre linealidad y funciones de activación.
Modelando relaciones no lineales
Aquí está la cosa: no importa cuántas capas agregues. Si todo lo que hacen es una suma ponderada no ganarás nada agregando más capas.
La razón es que el producto punto es una operación lineal. Si tienes varias capas realizando una suma ponderada, siempre puedes crear una red de una capa con exactamente el mismo comportamiento. Como ejemplo, mira la siguiente red:
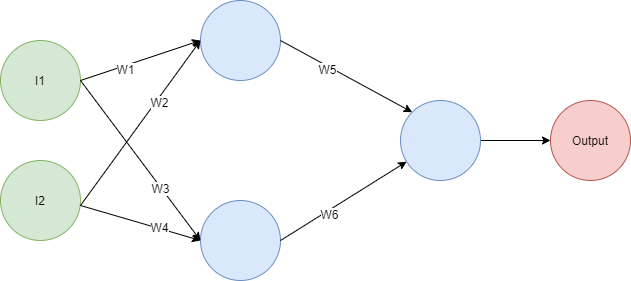
Si haces las matemáticas descubrirás que la salida está dada por la expresión Output = I1(W1W5+W3W6)+I2(W2W5+W4W6), así que puedes reemplazarla con esta red:
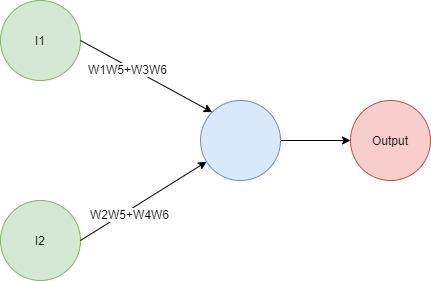
Redes más grandes podrían tomar un poco más de esfuerzo para compactar a mano debido a tener una ecuación más grande, pero el mismo principio aplica: no importa qué tan grande sea la red, siempre podrás reemplazarla con una red más pequeña.
Recuerda que originalmente queríamos crear capas extra para ayudarnos a construir una representación intermediaria de nuestros datos que tenga correlación con la salida. Lo que necesitamos es encontrar una forma de traer algo de no-linealidad a nuestra red para ampliar su espacio de hipótesis. Hacer esto nos ayudará a modelar comportamientos mucho más complejos y crear conjuntos intermedios que no estén atados a los patrones en las entradas.
Haremos esto aplicando una función de activación no lineal a las salidas de cada nodo. Hay muchas funciones diferentes que podemos elegir, pero dos funciones de activación populares son relu/rectifier y sigmoid.
En principio, podrías usar cualquier función como función de activación, pero no toda función será una buena elección. Las buenas funciones de activación satisfacen los siguientes criterios:
- Necesitan ser continuas y su dominio debe ser infinito.
- Necesitan ser monótonas (no cambiar de dirección)
- Necesitan ser no lineales.
- Necesitan ser fáciles de calcular.
Para nuestra implementación usaremos relu porque es simple y usualmente produce buenos resultados. Dado que relu es f(x) tenemos el siguiente comportamiento:
- f(x) = 0 si x<0
- f(x) = x si x>=0
En otras palabras, si la salida de un nodo es un número menor que 0 se convierte en 0. Si es mayor o igual que 0 reenvía la salida sin modificación.
Ahora podemos usar este conocimiento para crear una implementación completa en Python.
import numpy as nmpy
# Estos métodos ejecutan sobre arrays numpy
def relu(x):
return (x > 0) * x
def relu_deriv(prev_output):
return prev_output > 0
# Configuración de variables: usamos el array de numpy para crear una implementación más concisa
alpha = 0.1
hidden_layer_number_of_nodes = 4
weights_1 = nmpy.random.random((3 ,hidden_layer_number_of_nodes))
weights_2 = nmpy.random.random((hidden_layer_number_of_nodes))
inputs = nmpy.array([[1,1,1],
[1,1,0],
[0,1,0],
[0,1,1]
])
expected_values = nmpy.array([1,0,1,0])
run = 0
while True:
overall_run_error = 0
for input_set, expected_value in zip(inputs, expected_values):
# Estas son las salidas de la capa intermedia (la que tiene 4 nodos)
hidden_outputs = relu( nmpy.dot(input_set, weights_1) )
# Esta es la salida final, esto concluye el proceso de predicción
predicted_value = round(nmpy.dot(hidden_outputs, weights_2), 1)
# Ahora, calculamos los deltas y actualizamos los pesos usando
# la lógica que describimos anteriormente
layer2_delta = (predicted_value - expected_value)
# relu_deriv se asegura de que solo actualicemos nodos con salida > 0
layer1_delta = (weights_2 * layer2_delta) * relu_deriv(hidden_outputs)
weights_2 -= alpha * hidden_outputs.dot(layer2_delta)
weights_1 -= alpha * nmpy.outer(input_set, layer1_delta)
# Calculamos un error acumulado para cada ejecución
overall_run_error += nmpy.sum((predicted_value-expected_value) ** 2)
run += 1
## Imprimamos algunos datos de depuración
print("Los pesos en la capa final son: \n{}".format(weights_2) )
print("Los pesos en la primera capa son: \n{}".format(weights_1) )
print("El error general para la ejecución {} es {}\n\n".format(run, overall_run_error))
if overall_run_error == 0:
break
Ejecuta el código para verificar que converge a una solución con 0 error:
Los pesos en la capa final son:
[ 0.13677727 0.29952828 -0.09968558 0.56497112]
Los pesos en la primera capa son:
[[ 0.68186112 -0.07723001 0.61481898 0.01363698]
[ 0.28297269 -0.07377539 0.00576834 0.54298254]
[ 0.57557199 0.41983547 0.57342688 0.13776574]]
El error general para la ejecución 1 es 4.95
Los pesos en la capa final son:
[ 0.10819863 0.28437992 -0.12201187 0.54867314]
Los pesos en la primera capa son:
[[ 0.67741254 -0.06524888 0.6134278 0.0065985 ]
[ 0.27715933 -0.08351396 0.00435572 0.53331793]
[ 0.56920599 0.4100969 0.5751969 0.11835256]]
El error general para la ejecución 2 es 1.39
...
Los pesos en la capa final son:
[-0.26000191 1.74695864 -0.55762033 1.03700425]
Los pesos en la primera capa son:
[[ 0.4874603 1.06748941 0.5756712 -0.46733342]
[ 0.07043213 -1.10048561 -0.00235896 0.9503538 ]
[ 0.45488944 1.09249163 0.63419715 -0.44475593]]
El error general para la ejecución 147 es 0.019999999999999997
Los pesos en la capa final son:
[-0.26000191 1.74695864 -0.55762033 1.03700425]
Los pesos en la primera capa son:
[[ 0.4874603 1.06748941 0.5756712 -0.46733342]
[ 0.07043213 -1.10048561 -0.00235896 0.9503538 ]
[ 0.45488944 1.09249163 0.63419715 -0.44475593]]
El error general para la ejecución 148 es 0.0
Deep learning, redes profundas
Ahora conocemos todas las piezas fundamentales necesarias para entender el deep learning. La principal diferencia entre las redes neuronales tradicionales y las arquitecturas modernas de deep learning es el gran número de capas.
Hasta hace poco entrenar redes con enormes números de entradas y capas no era posible, pero gracias a computadoras poderosas y el ingenio de los científicos de la computación ahora podemos resolver problemas novedosos usando esta poderosa idea.
En el fondo, las arquitecturas de deep-learning construyen representaciones intermedias de las entradas que modelan la presencia o ausencia de características particulares. Piensa en una red encargada de identificar caras de perros, tal red probablemente tendrá capas intermedias detectando la presencia de narices, orejas y ojos de perro, entre muchas otras características. Una capa final toma en consideración todos los resultados anteriores para emitir un veredicto.
¡Gracias por leer!
Qué hacer después
- Comparte este artículo con amigos y colegas. Gracias por ayudarme a llegar a personas que podrían encontrar esta información útil.
- Este artículo está basado en el libro: Grokking Deep Learning y en Deep Learning (Goodfellow, Bengio, Courville).
- Puedes encontrar el código fuente para esta serie aquí
- Envíame un email con preguntas, comentarios o sugerencias (está en la página Autor)
