En el artículo anterior establecimos las bases para una implementación generalizada del descenso de gradiente. Es decir, casos con múltiples entradas y una salida, y múltiples salidas y una entrada.
En este artículo, continuaremos nuestros esfuerzos de generalización para crear una versión del descenso de gradiente que funcione con cualquier cantidad de entradas y salidas.
Primero, crearemos una implementación paso a paso para solo 3 entradas y 3 salidas. A partir de esto, extrapolaremos otra implementación que soporte cualquier cantidad de entradas y salidas.
Descenso de gradiente: Múltiples entradas - múltiples salidas.
El descenso de gradiente generalizado para una red con múltiples entradas usa una combinación de los enfoques utilizados en los dos casos anteriores.
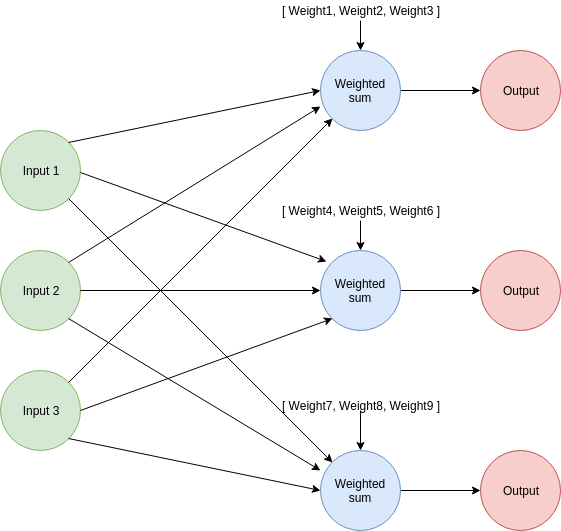
- Como en el caso de múltiples entradas/1 salida, realizarás correcciones a pesos individuales multiplicando sus respectivas entradas por un factor común
alpha * (valor_predicho - valor_esperado). - Como en el caso de 1 entrada/múltiples salidas, puedes visualizar cada uno de esos subsistemas peso-salida como redes neuronales individuales.
Todo se trata de calcular un factor de ajuste para cada peso usando los valores correctos. Cada cálculo de ajuste de peso debe involucrar solo valores (entrada, valor esperado, valor predicho) relacionados con su peso particular.
Implementación paso a paso de una red 3x3
Échale un vistazo al diagrama si tienes problemas visualizando las partes de la red.
Para nuestra implementación:
- Configuraremos las variables necesarias y tendremos un bucle de ajuste de pesos, tal como hicimos en todos los casos anteriores.
- En la primera parte del bucle de optimización, calcularemos las predicciones para todas las salidas. Después, calcularemos el error en cada predicción usando los valores esperados respectivos.
- Calcularemos el factor de ajuste de peso para cada uno de nuestros 9 pesos y realizaremos los ajustes requeridos.
- Verificaremos si los valores de error suman 0 (o muy cerca de 0). Con esta información, podemos decidir si nuestras predicciones son lo suficientemente buenas o si necesitamos mantener el bucle de optimización funcionando.
Como mencionamos antes, realizaremos las predicciones y ajustes como si estuviéramos tratando con 3 subredes con los mismos valores de entrada.
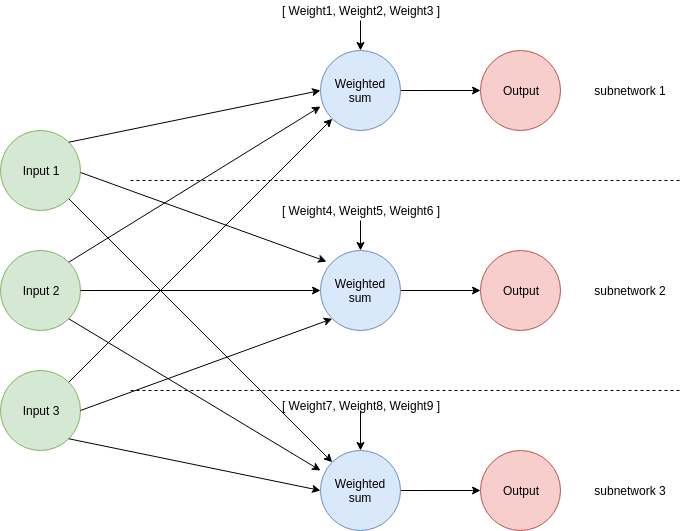
Configuración de variables
El primer paso es crear nuestras variables:
alpha = 0.2
inputs = [0.2, 2.3, 1.2]
expected_values = [8, 46, 0.1]
weights_1 = [7.1, 1.1, 4.4] # Pesos para la primera salida
weights_2 = [5.7, 3, 9.1] # Pesos para la segunda salida
weights_3 = [2.2, 5.3, 7] # Pesos para la tercera salida
weights = [weights_1, weights_2, weights_3]
El orden es importante: La primera entrada en los valores esperados corresponde al primer valor esperado. Además, nota que ponemos todos los pesos en un array bidimensional. Como imaginaste, los primeros 3 pesos producen la primera salida (relacionada con el primer valor esperado/predicho), y así sucesivamente.
Cálculo de predicción y error
Ahora es momento para los pasos de cálculo de predicción y error. Escribiremos una función de red neuronal de múltiples salidas para calcular cada una de las salidas.
# En artículos anteriores explicamos cómo funciona esto
def dot_product(first_vector, second_vector):
assert( len(first_vector) == len(second_vector))
vectors_size = len(first_vector)
dot_product_result = 0
for index in range(vectors_size):
dot_product_result += first_vector[index] * second_vector[index]
return round(dot_product_result, 2)
def multi_input_multi_output_neural_network(inputs, weights):
predicted_values= []
for weights_for_estimate in weights:
predicted_values.append( dot_product(inputs, weights_for_estimate) )
return predicted_values
#...
#Esto sucede dentro del bucle de actualización de pesos
predicted_values = multi_input_multi_output_neural_network(inputs, weights)
error_1 = (predicted_values[0] - expected_values[0])**2
error_2 = (predicted_values[1] - expected_values[1])**2
error_3 = (predicted_values[2] - expected_values[2])**2
La función de predicción realiza las mismas operaciones que ya conocemos: toma los pesos que pertenecen a la primera subred (la de arriba en la imagen) y estima la primera salida. Después, realiza la misma operación para la 2da y 3ra subredes. Cada salida (valor predicho) se pone en el array devuelto en el orden en que fueron calculadas.
Este orden es importante para mantener consistencia en nuestros cálculos. Como resultado podemos calcular cada error como error_N = (predicted_values[N] - expected_values[N])**2.
Ahora podemos lidiar con la parte de ajuste de pesos usando las fórmulas que ya conocemos.
Ajustando pesos
Recuerda que calculamos el nuevo valor de un peso como:
weight -= alpha * input * (predicted_value - expected_value)
Repasemos qué significan estos:
- alpha es una tasa de aprendizaje que nos ayuda a regular la velocidad de aprendizaje y prevenir el sobreajuste.
- input es el valor de la entrada que fue multiplicado por el peso que estamos actualizando actualmente.
- predicted_value es la salida que nuestro peso participó en producir.
- expected_value es el valor esperado asociado con el predicted_value.
Aplicar descenso de gradiente para redes neuronales con múltiples entradas y salidas es solo una cuestión de aplicar esa ecuación a cada peso en la red usando los valores correctos.
Veamos el código para el ajuste de los pesos para la primera subred:
weight_adjustment_1 = alpha * inputs[0] * (predicted_values[0] - expected_values[0])
weight_adjustment_2 = alpha * inputs[1] * (predicted_values[0] - expected_values[0])
weight_adjustment_3 = alpha * inputs[2] * (predicted_values[0] - expected_values[0])
weights[0][0] -= weight_adjustment_1
weights[0][1] -= weight_adjustment_2
weights[0][2] -= weight_adjustment_3
El código se explica por sí mismo, pero presta atención a los siguientes detalles:
- Porque nuestros pesos están colocados en un array bidimensional, usamos el primer índice (en este caso 0) para especificar con qué conjunto de pesos estamos trabajando. El segundo índice nos dice el peso específico. Por ejemplo
weights[0][0]significa primera subred, primer peso. - El factor weight_adjustment usa la entrada que su respectivo peso multiplicó cuando produjo la salida.
- alpha es el mismo para todos.
- Las ecuaciones usan solo los primeros valores (índice 0) para valor predicho y valor esperado porque esos son los predichos y esperados por la primera subred.
Veamos ahora el proceso de ajuste de pesos de la segunda subred (del medio):
weight_adjustment_4 = alpha * inputs[0] * (predicted_values[1] - expected_values[1])
weight_adjustment_5 = alpha * inputs[1] * (predicted_values[1] - expected_values[1])
weight_adjustment_6 = alpha * inputs[2] * (predicted_values[1] - expected_values[1])
weights[1][0] -= weight_adjustment_4
weights[1][1] -= weight_adjustment_5
weights[1][2] -= weight_adjustment_6
- Nota que el primer índice al referirse a la variable weights es 1. Esto significa que ahora estamos tratando con la 2da subred.
- El factor weight_adjustment usa la entrada que su respectivo peso multiplicó cuando produjo la salida.
- alpha sigue siendo el mismo.
- Las ecuaciones usan solo los segundos valores (índice 1) para valor predicho y valor esperado porque esos son los predichos y esperados por la segunda subred.
Ahora que tienes una idea de qué significa multiplicado por los valores correctos, puedes entender qué está pasando con los últimos 3 pesos en nuestra red neuronal.
weight_adjustment_7 = alpha * inputs[0] * (predicted_values[2] - expected_values[2])
weight_adjustment_8 = alpha * inputs[1] * (predicted_values[2] - expected_values[2])
weight_adjustment_9 = alpha * inputs[2] * (predicted_values[2] - expected_values[2])
weights[2][0] -= weight_adjustment_7
weights[2][1] -= weight_adjustment_8
weights[2][2] -= weight_adjustment_9
Decidiendo cuándo parar
Seguimos manteniendo el mismo criterio para el éxito: ajustar los valores de nuestros pesos hasta que los valores de error sean 0 o estén cerca de 0. La forma más simple de averiguar si tenemos éxito es sumando todos los errores y verificando si son 0. Si lo son, podemos romper el ciclo:
if(error_1 + error_2 + error_3 == 0):
break
Juntándolo todo
La implementación final de nuestra red neuronal de 3 entradas/3 salidas se ve así:
def dot_product(first_vector, second_vector):
assert( len(first_vector) == len(second_vector))
vectors_size = len(first_vector)
dot_product_result = 0
for index in range(vectors_size):
dot_product_result += first_vector[index] * second_vector[index]
return round(dot_product_result, 2)
def multi_input_multi_output_neural_network(inputs, weights):
predicted_values= []
for weights_for_estimate in weights:
predicted_values.append( dot_product(inputs, weights_for_estimate) )
return predicted_values
alpha = 0.2
inputs = [0.2, 2.3, 1.2]
expected_values = [8, 46, 0.1]
weights_1 = [7.1, 1.1, 4.4] # Pesos para la primera salida
weights_2 = [5.7, 3, 9.1] # Pesos para la segunda salida
weights_3 = [2.2, 5.3, 7] # Pesos para la tercera salida
weights = [weights_1, weights_2, weights_3]
while True:
predicted_values = multi_input_multi_output_neural_network(inputs, weights)
print("Según mi red neuronal, el 1er resultado es {}".format(predicted_values[0]))
print("Según mi red neuronal, el 2do resultado es {}".format(predicted_values[1]))
print("Según mi red neuronal, el 3er resultado es {}".format(predicted_values[2]))
error_1 = (predicted_values[0] - expected_values[0])**2
error_2 = (predicted_values[1] - expected_values[1])**2
error_3 = (predicted_values[2] - expected_values[2])**2
print("El error en la 1era predicción es {} ".format(error_1))
print("El error en la 2da predicción es {} ".format(error_2))
print("El error en la 3era predicción es {} ".format(error_3))
## Estos pesos participaron en la predicción del primer valor de salida
weight_adjustment_1 = alpha * inputs[0] * (predicted_values[0] - expected_values[0])
weight_adjustment_2 = alpha * inputs[1] * (predicted_values[0] - expected_values[0])
weight_adjustment_3 = alpha * inputs[2] * (predicted_values[0] - expected_values[0])
weights[0][0] -= weight_adjustment_1
weights[0][1] -= weight_adjustment_2
weights[0][2] -= weight_adjustment_3
print("\n")
print("El 1er peso para la primera salida es ahora {} ".format(weights[0][0]) )
print("El 2do peso para la primera salida es ahora {} ".format(weights[0][1]) )
print("El 3er peso para la primera salida es ahora {} ".format(weights[0][2]) )
## Estos pesos participaron en la predicción del segundo valor de salida
weight_adjustment_4 = alpha * inputs[0] * (predicted_values[1] - expected_values[1])
weight_adjustment_5 = alpha * inputs[1] * (predicted_values[1] - expected_values[1])
weight_adjustment_6 = alpha * inputs[2] * (predicted_values[1] - expected_values[1])
weights[1][0] -= weight_adjustment_4
weights[1][1] -= weight_adjustment_5
weights[1][2] -= weight_adjustment_6
print("\n")
print("El 1er peso para la segunda salida es ahora {} ".format(weights[1][0]) )
print("El 2do peso para la segunda salida es ahora {} ".format(weights[1][1]) )
print("El 3er peso para la segunda salida es ahora {} ".format(weights[1][2]) )
## Estos pesos participaron en la predicción del tercer valor de salida
weight_adjustment_7 = alpha * inputs[0] * (predicted_values[2] - expected_values[2])
weight_adjustment_8 = alpha * inputs[1] * (predicted_values[2] - expected_values[2])
weight_adjustment_9 = alpha * inputs[2] * (predicted_values[2] - expected_values[2])
weights[2][0] -= weight_adjustment_7
weights[2][1] -= weight_adjustment_8
weights[2][2] -= weight_adjustment_9
print("\n")
print("El 1er peso para la tercera salida es ahora {} ".format(weights[2][0]) )
print("El 2do peso para la tercera salida es ahora {} ".format(weights[2][1]) )
print("El 3er peso para la tercera salida es ahora {} ".format(weights[2][2]) )
print("\n")
#Paramos cuando todos los errores son 0
if(error_1 + error_2 + error_3 == 0):
break
Puedes verificar que esta red funciona ejecutando el código y revisando tu terminal:
Según mi red neuronal, el 1er resultado es 9.23
Según mi red neuronal, el 2do resultado es 18.96
Según mi red neuronal, el 3er resultado es 21.03
El error en la 1era predicción es 1.512900000000001
El error en la 2da predicción es 731.1615999999999
El error en la 3era predicción es 438.06489999999997
El 1er peso para la primera salida es ahora 7.0508
El 2do peso para la primera salida es ahora 0.5341999999999999
El 3er peso para la primera salida es ahora 4.1048
El 1er peso para la segunda salida es ahora 6.7816
El 2do peso para la segunda salida es ahora 15.438399999999998
El 3er peso para la segunda salida es ahora 15.589599999999999
El 1er peso para la tercera salida es ahora 1.3628
El 2do peso para la tercera salida es ahora -4.327799999999999
El 3er peso para la tercera salida es ahora 1.9768
Según mi red neuronal, el 1er resultado es 7.56
Según mi red neuronal, el 2do resultado es 55.57
Según mi red neuronal, el 3er resultado es -7.31
El error en la 1era predicción es 0.19360000000000036
El error en la 2da predicción es 91.5849
El error en la 3era predicción es 54.90809999999999
El 1er peso para la primera salida es ahora 7.0684
El 2do peso para la primera salida es ahora 0.7366
El 3er peso para la primera salida es ahora 4.2104
El 1er peso para la segunda salida es ahora 6.3988
El 2do peso para la segunda salida es ahora 11.036199999999997
El 3er peso para la segunda salida es ahora 13.2928
El 1er peso para la tercera salida es ahora 1.6592
El 2do peso para la tercera salida es ahora -0.9191999999999996
El 3er peso para la tercera salida es ahora 3.7551999999999994
... Más iteraciones
Según mi red neuronal, el 1er resultado es 8.0
Según mi red neuronal, el 2do resultado es 46.0
Según mi red neuronal, el 3er resultado es 0.1
El error en la 1era predicción es 0.0
El error en la 2da predicción es 0.0
El error en la 3era predicción es 0.0
El 1er peso para la primera salida es ahora 7.063599999999999
El 2do peso para la primera salida es ahora 0.6814000000000001
El 3er peso para la primera salida es ahora 4.1816
El 1er peso para la segunda salida es ahora 6.498799999999999
El 2do peso para la segunda salida es ahora 12.186199999999996
El 3er peso para la segunda salida es ahora 13.8928
El 1er peso para la tercera salida es ahora 1.5816
El 2do peso para la tercera salida es ahora -1.8115999999999994
El 3er peso para la tercera salida es ahora 3.2895999999999996
Implementación paso a paso de una red generalizada
Generalizar para cualquier número de entradas y salidas se puede hacer tomando nuestra implementación básica 3x3 y refactorizándola para trabajar con vectores. Podemos hacer esto creando funciones que operen en colecciones de elementos en lugar de aplicar las ecuaciones una por una.
Configuración de variables
Nuestra configuración de variables no necesita ningún cambio, ya que todas están puestas en vectores. Démosle una palmadita en la espalda por ser visionarios y entender la importancia de las colecciones.
Cálculo de predicción y error
La parte de predicción no necesita ninguna actualización. Estamos usando una función de predicción generalizada que funciona con cualquier número de entradas y salidas, así que no hay nada que cambiar ahí.
Para el cálculo de errores, necesitamos crear una función que reciba un array de valores predichos y valores esperados y devuelva un nuevo array con los errores:
def calculate_errors(predicted_values, expected_values):
errors = []
for predicted_value, expected_value in zip(predicted_values, expected_values):
error = (predicted_value - expected_value)**2
errors.append(error)
return errors
#...
# Nuestras 3 líneas anteriores son ahora solo una
errors = calculate_errors(predicted_values, expected_values)
Ajustando pesos
El proceso de ajuste de pesos tiene dos partes principales:
- Calcular los factores de ajuste de peso para cada peso.
- Restar cada factor de ajuste de su respectivo peso.
Esto es más fácil de visualizar en forma matricial: Imagina que tenemos una matriz de pesos y una matriz de factores de ajuste. Actualizar los pesos es solo una cuestión de calcular la segunda matriz y restarla de la primera.
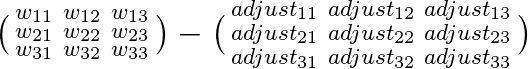
Los valores para las matrices de ajuste no son secretos, ya los calculamos en nuestra primera implementación. La única diferencia es que en lugar de calcularlos uno por uno, los calcularemos en un array 2d. En nuestro ejemplo 3x3, la matriz de ajuste se ve así:
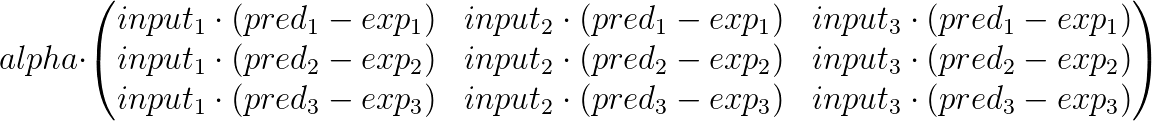
Esta matriz es solo un arreglo de los valores de corrección que calculamos uno por uno en la primera implementación. Algunas cosas que podrían ayudarte a entenderla un poco mejor son:
- Nota que alpha está multiplicando cada entrada individual en la matriz.
- Cada fila representa los valores de corrección asociados con una sola salida. Por eso la primera fila solo trata con los valores esperados y predichos para la primera salida y así sucesivamente.
- Cada columna es multiplicada por una entrada específica, todos los pesos en esa columna fueron multiplicados por esa entrada para producir una predicción.
- Si aumentas el número de entradas la matriz se vuelve más ancha, si aumentas el número de salidas se vuelve más alta.
Solo necesitamos implementar una función que calcule estos valores cuando se le den alpha, un array para valores esperados y un array de valores predichos y entradas:
def calculate_weight_correction_matrix(alpha, inputs, expected_values, predicted_values):
weight_correction_factors = []
#Calcula factores fila por fila
for exp, pred in zip(expected_values, predicted_values):
row = []
delta = (pred - exp) * alpha
for input in inputs:
row.append( input * delta )
weight_correction_factors.append(row)
return weight_correction_factors
El siguiente paso es más fácil, solo necesitamos crear una función que reste esta matriz de factores de corrección de la matriz de pesos:
def calculate_corrected_weights(weights, correction_factors):
updated_weights = []
for row_weight, row_correction in zip(weights, correction_factors):
row = []
for weight, correction in zip(row_weight, row_correction):
row.append( weight - correction )
updated_weights.append(row)
return updated_weights
Con esto en su lugar, todas las líneas anteriores para corregir valores de pesos se pueden reducir a solo dos. Es más, ya no estamos limitados a redes neuronales 3x3:
weight_correction_factors = calculate_weight_correction_matrix(alpha, inputs, expected_values, predicted_values)
weights = calculate_corrected_weights(weights, weight_correction_factors)
Después, decidir cuándo parar.
Decidiendo cuándo parar
Esta es otra implementación fácil: solo necesitamos una función que devuelva la suma de cada peso en el array de errores.
def calculate_total_error(errors):
return sum(errors)
# ...
if(calculate_total_error(errors) == 0):
break
¡Listo!
Juntándolo todo
Después de aplicar todos los cambios, esta es la versión final del código:
def dot_product(first_vector, second_vector):
assert( len(first_vector) == len(second_vector))
vectors_size = len(first_vector)
dot_product_result = 0
for index in range(vectors_size):
dot_product_result += first_vector[index] * second_vector[index]
return round(dot_product_result, 2)
def multi_input_multi_output_neural_network(inputs, weights):
predicted_values= []
for weights_for_estimate in weights:
predicted_values.append( dot_product(inputs, weights_for_estimate) )
return predicted_values
def calculate_errors(predicted_values, expected_values):
errors = []
for predicted_value, expected_value in zip(predicted_values, expected_values):
error = (predicted_value - expected_value)**2
errors.append(error)
return errors
def calculate_weight_correction_matrix(alpha, inputs, expected_values, predicted_values):
weight_correction_factors = []
#Calcula factores fila por fila
for exp, pred in zip(expected_values, predicted_values):
row = []
delta = (pred - exp) * alpha
for input in inputs:
row.append( input * delta )
weight_correction_factors.append(row)
return weight_correction_factors
def calculate_corrected_weights(weights, correction_factors):
updated_weights = []
for row_weight, row_correction in zip(weights, correction_factors):
row = []
for weight, correction in zip(row_weight, row_correction):
row.append( weight - correction )
updated_weights.append(row)
return updated_weights
def calculate_total_error(errors):
return sum(errors)
alpha = 0.2
inputs = [0.2, 2.3, 1.2]
expected_values = [8, 46, 0.1]
weights_1 = [7.1, 1.1, 4.4] # Pesos para la primera salida
weights_2 = [5.7, 3, 9.1] # Pesos para la segunda salida
weights_3 = [2.2, 5.3, 7] # Pesos para la tercera salida
weights = [weights_1, weights_2, weights_3]
while True:
predicted_values = multi_input_multi_output_neural_network(inputs, weights)
print("Según mi red neuronal, el 1er resultado es {}".format(predicted_values[0]))
print("Según mi red neuronal, el 2do resultado es {}".format(predicted_values[1]))
print("Según mi red neuronal, el 3er resultado es {}".format(predicted_values[2]))
errors = calculate_errors(predicted_values, expected_values)
print("El error en la 1era predicción es {} ".format(errors[0]))
print("El error en la 2da predicción es {} ".format(errors[1]))
print("El error en la 3era predicción es {} ".format(errors[2]))
## Estos pesos participaron en la predicción del primer valor de salida
weight_correction_factors = calculate_weight_correction_matrix(alpha, inputs, expected_values, predicted_values)
weights = calculate_corrected_weights(weights, weight_correction_factors)
print("\n")
print("El 1er peso para la primera salida es ahora {} ".format(weights[0][0]) )
print("El 2do peso para la primera salida es ahora {} ".format(weights[0][1]) )
print("El 3er peso para la primera salida es ahora {} ".format(weights[0][2]) )
print("\n")
print("El 1er peso para la segunda salida es ahora {} ".format(weights[1][0]) )
print("El 2do peso para la segunda salida es ahora {} ".format(weights[1][1]) )
print("El 3er peso para la segunda salida es ahora {} ".format(weights[1][2]) )
print("\n")
print("El 1er peso para la tercera salida es ahora {} ".format(weights[2][0]) )
print("El 2do peso para la tercera salida es ahora {} ".format(weights[2][1]) )
print("El 3er peso para la tercera salida es ahora {} ".format(weights[2][2]) )
print("\n")
#Paramos cuando todos los errores son 0
if(calculate_total_error(errors) == 0):
break
Ejecutar este código producirá los mismos resultados que nuestra primera versión. La ventaja es que ahora tenemos una implementación del descenso de gradiente que puede lidiar con cualquier número de entradas y salidas!
Ahora conoces el descenso de gradiente
Si llegaste hasta aquí, ¡felicitaciones!
En los últimos tres artículos, exploramos (diseccionamos) el descenso de gradiente. Puede parecer excesivamente complicado al principio, pero es una técnica increíblemente poderosa con una enorme gama de aplicaciones en ciencia de datos y machine learning.
Este artículo es bastante grande y denso, pero si llegaste hasta aquí ya tienes un entendimiento mucho mejor del descenso de gradiente. Traté de ir paso a paso tanto como fuera posible, algo que esperamos haya hecho el artículo más fácil de entender.
Ahora que la mayoría del trabajo de base se ha establecido, podemos comenzar a tratar con cosas más de deep-learning.
¡Gracias por leer!
Qué hacer después
- Comparte este artículo con amigos y colegas. Gracias por ayudarme a llegar a personas que podrían encontrar esta información útil.
- Este artículo está basado en el libro: Grokking Deep Learning y en Deep Learning (Goodfellow, Bengio, Courville).
- Puedes encontrar el código fuente para esta serie aquí
- Envíame un email con preguntas, comentarios o sugerencias (está en la página Autor)
