En el artículo anterior, aprendimos sobre el descenso de gradiente con una red simple de 1-entrada/1-salida. En este artículo, aprenderemos cómo generalizar esta técnica para redes con cualquier número de entradas y salidas.
Nos concentraremos en 3 escenarios diferentes:
- Descenso de gradiente en redes neuronales con múltiples entradas y una sola salida.
- Descenso de gradiente en redes neuronales con una sola entrada y múltiples salidas
- Finalmente, aprenderemos cómo usar el descenso de gradiente con múltiples entradas y múltiples salidas
Para hacer las cosas más fáciles lo dividiremos en dos artículos. Este tratará los primeros dos escenarios y sentará las bases para el artículo de la próxima semana donde implementaremos el tercer escenario.
Hagamos un pequeño repaso del descenso de gradiente.
Repaso del descenso de gradiente para 1-entrada/1-salida
Todos los escenarios de descenso de gradiente que estudiaremos son variaciones del caso de 1-entrada y 1-salida. Entender el caso base en profundidad te ayudará a entender el siguiente material, así que hagamos un repaso rápido:
- Configuración: Tienes un conjunto de entrenamiento que te dice qué resultado (valor esperado) una entrada dada debería producir. Este valor esperado se usa para calcular el error en la predicción de tu red. Se establecen valores iniciales aleatorios para los pesos de tu red.
- Predicción: Pasas la entrada a tu red neuronal y usas el valor inicial de tu(s) peso(s) para producir una estimación (valor predicho)
- Evaluación del error: Calculas qué tan desviada está tu predicción usando la ecuación para el error, que te dice qué tan lejos está el valor predicho del valor esperado.
- Corrección: Calculas cuánto necesitas ajustar tu(s) peso(s). Es el producto de los valores de derivada, entrada y alpha.
- Iterar: Usando el valor del error, decides qué hacer después. Si el error es 0 (o cercano) puedes decir que los pesos actuales son lo suficientemente buenos. Si no, puedes regresar al paso 2 y ejecutar otro ciclo de ajuste de pesos.
Estos 5 pasos serán nuestro andamiaje mental para el proceso de aprendizaje de la red. Al tratar con una nueva configuración (multi-entrada, multi-salida, o ambas), identificaremos qué es diferente y adaptaremos el proceso.
Como verás a continuación, el paso afectado usualmente es el 4 porque la forma en que calculamos el factor de corrección para cada peso cambia un poco dependiendo de la topología de la red.
Descenso de gradiente: Múltiples entradas - una salida.
Veamos cómo se ve una red con múltiples entradas y una sola salida:
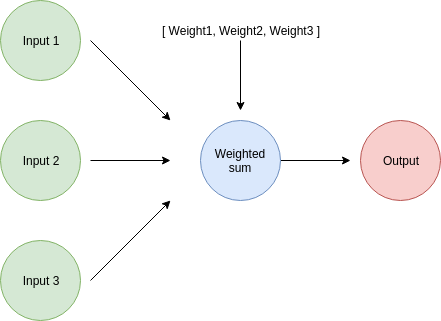
Una red con muchas entradas y solo una salida tiene un peso asociado con cada una de las entradas. Esto significa que necesitaremos calcular el factor de corrección de peso para cada una de ellas.
derivative = input * (predicted_value - expected_value)
weight_adjustment = alpha * derivative
weight -= weight_adjustment
O de una forma más concisa:
weight_adjustment = input * alpha * (predicted_value - expected_value)
weight -= weight_adjustment
Así es como calculamos el factor de corrección para cada peso individual: cada peso es responsable de una entrada, así que el cálculo para cada corrección involucrará su respectiva entrada:
weight_adjustment_1 = input_1 * alpha * (predicted_value - expected_value)
weight_1 -= weight_adjustment_1
weight_adjustment_2 = input_2 * alpha * (predicted_value - expected_value)
weight_2 -= weight_adjustment_2
weight_adjustment_3 = input_3 * alpha * (predicted_value - expected_value)
weight_3 -= weight_adjustment_3
Nota cómo cada ajuste involucra una parte compartida (alpha * (predicted_value - expected_value)) y una parte específica que usa el peso y su respectiva entrada.
Esta implementación obviamente no es lo suficientemente buena. ¿Qué pasa si tenemos miles de entradas? Podemos realizar fácilmente estas actualizaciones para cualquier número de entradas/pesos si los manejamos como vectores.
Creemos métodos para calcular el factor de corrección y para ajustar el valor de cada peso:
def calculate_weight_adjustments(inputs, correction_factor):
weight_adjustments = []
for input in inputs:
weight_adjustment = input * correction_factor
weight_adjustments.append(weight_adjustment)
return weight_adjustments
def calculate_updated_weights(weights, weight_adjustments):
updated_wights = []
for weight, weight_adjustment in zip(weights, weight_adjustments):
updated_wight = weight - weight_adjustment
updated_wights.append(updated_wight)
return updated_wights
Lo único ‘extraño’ en estos dos métodos es el argumento correction_factor. Es solo un nombre que le di al factor alpha * (predicted_value - expected_value) que mencionamos antes.
Con esas funciones en su lugar, la implementación final es muy similar al caso base. En lugar de ajustar solo un peso a la vez, podemos ajustar todo el vector de pesos:
correction_factor = alpha * (predicted_value - expected_value)
weight_adjustments = calculate_weight_adjustments(inputs, correction_factor )
weights = calculate_updated_weights(weights, weight_adjustments)
Este es un ejemplo completo de descenso de gradiente aplicado a una red neuronal multi-entrada con una sola salida:
# Las 2 funciones definidas arriba (calculate_weight_adjustments y calculate_updated_weights) van aquí
# Nuestra confiable implementación de red neuronal multi-entrada
def multi_input_neural_network(inputs, weights):
assert( len(inputs) == len(weights))
predicted_value = 0
for input, weight in zip(inputs, weights):
predicted_value += input * weight
return predicted_value
inputs = [0.2, 4, 0.1]
weights = [10, 2, 11]
expected_value = 8
alpha = 0.04
while True:
# Debido a cómo python maneja punto flotante, redondeamos los valores
predicted_value = round(multi_input_neural_network(inputs, weights), 2)
print("Según mi red neuronal, el resultado es {}".format(predicted_value))
error = (predicted_value - expected_value)**2
print("El error en la predicción es {} ".format(error))
correction_factor = alpha * (predicted_value - expected_value)
weight_adjustments = calculate_weight_adjustments(inputs, correction_factor )
print("Estos son los valores de ajuste de peso: {}".format(weight_adjustments))
weights = calculate_updated_weights(weights, weight_adjustments)
print("Estos son los nuevos pesos: {}".format(weights))
print("\n")
if(error == 0):
break
Ejecutar este código con un alpha de 0.04 resultará en la siguiente iteración de aprendizaje:
Según mi red neuronal, el resultado es 11.1
El error en la predicción es 9.609999999999998
Estos son los valores de ajuste de peso: [0.0248, 0.49599999999999994, 0.0124]
Estos son los nuevos pesos: [9.9752, 1.504, 10.9876]
... Más iteraciones
Según mi red neuronal, el resultado es 8.01
El error en la predicción es 9.999999999999574e-05
Estos son los valores de ajuste de peso: [7.999999999999831e-05, 0.001599999999999966, 3.9999999999999156e-05]
Estos son los nuevos pesos: [9.961359999999999, 1.2271999999999998, 10.98068]
Según mi red neuronal, el resultado es 8.0
El error en la predicción es 0.0
Estos son los valores de ajuste de peso: [0.0, 0.0, 0.0]
Estos son los nuevos pesos: [9.961359999999999, 1.2271999999999998, 10.98068]
El descenso de gradiente para múltiples entradas es fácil de entender si ya internalizaste cómo funciona para el caso base. La única diferencia es que realizamos actualizaciones en cada par peso/entrada individual.
Descenso de gradiente: Una entrada - múltiples salidas.
Echemos un vistazo al caso opuesto, donde tenemos una red neuronal con una sola entrada y múltiples salidas.
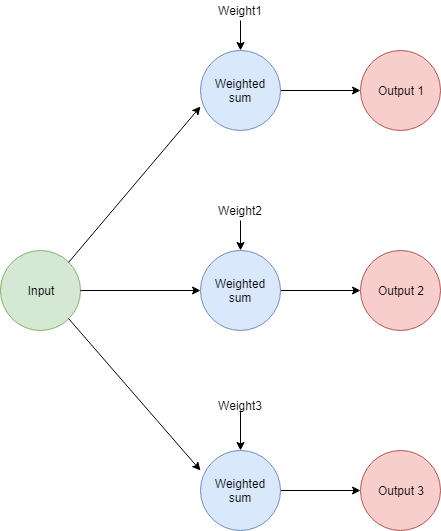
La forma más fácil de visualizar este escenario es ver cada par peso/salida como una sola red neuronal. La principal diferencia es que cada una de ellas tendrá sus propios valores predichos y esperados. Esos valores se usarán para calcular los ajustes de peso para la respectiva sub-red.
Esto básicamente significa que estamos ejecutando el caso 1-entrada/1-salida 3 veces. Una implementación ingenua para el caso de 3-salidas se ve así:
# Esto pasa dentro de un bucle como en los otros casos
# Primero, calculamos la predicción para cada valor individual
predicted_value_1 = round(neural_network(input, weight_1), 2)
predicted_value_2 = round(neural_network(input, weight_2), 2)
predicted_value_3 = round(neural_network(input, weight_3), 2)
# Cada valor predicho tendrá su propio error de predicción asociado
error_1 = (predicted_value_1 - expected_value_1)**2
error_2 = (predicted_value_2 - expected_value_2)**2
error_3 = (predicted_value_3 - expected_value_3)**2
# Después, podemos usar esta información para calcular la derivada para cada uno de los 3 casos
derivative_1 = input * (predicted_value_1 - expected_value_1)
derivative_2 = input * (predicted_value_2 - expected_value_2)
derivative_3 = input * (predicted_value_3 - expected_value_3)
# La información previamente calculada ahora se usa para actualizar el valor de nuestros pesos
weight_adjustment_1 = alpha * derivative_1
weight_adjustment_2 = alpha * derivative_2
weight_adjustment_3 = alpha * derivative_3
weight_1 -= weight_adjustment_1
weight_2 -= weight_adjustment_2
weight_3 -= weight_adjustment_3
La implementación completa (este enfoque ingenuo) se puede encontrar en el código fuente del artículo. Ejecutémosla para verificar que modifica los pesos hasta que predice correctamente las salidas.
Según mi red neuronal, el 1er resultado es 2.0
Según mi red neuronal, el 2do resultado es 4.0
Según mi red neuronal, el 3er resultado es 0.6
El error en la 1ra predicción es 36.0
El error en la 2da predicción es 1764.0
El error en la 3ra predicción es 0.25
El valor de nuestra derivada para el 1er peso=10 es -1.2000000000000002
El valor de nuestra derivada para el 2do peso=20 es -8.4
El valor de nuestra derivada para el 3er peso=3 es 0.1
El nuevo valor de nuestro 1er peso es 38.800000000000004
El nuevo valor de nuestro 2do peso es 221.60000000000002
El nuevo valor de nuestro 3er peso es 0.5999999999999996
... Más iteraciones
Según mi red neuronal, el 1er resultado es 8.0
Según mi red neuronal, el 2do resultado es 46.0
Según mi red neuronal, el 3er resultado es 0.1
El error en la 1ra predicción es 0.0
El error en la 2da predicción es 0.0
El error en la 3ra predicción es 0.0
El valor de nuestra derivada para el 1er peso=40.00000000000001 es 0.0
El valor de nuestra derivada para el 2do peso=230.00000000000003 es 0.0
El valor de nuestra derivada para el 3er peso=0.5039999999999997 es 0.0
El nuevo valor de nuestro 1er peso es 40.00000000000001
El nuevo valor de nuestro 2do peso es 230.00000000000003
El nuevo valor de nuestro 3er peso es 0.5039999999999997
Sí, tienes razón, esta implementación es bastante incómoda y realmente no funciona más allá de 3 salidas. Como antes, creemos algunas funciones que manejen todos estos cálculos en vectores:
def calculate_errors(predicted_values, expected_values):
errors = []
for pred_value, exp_value in zip(predicted_values, expected_values):
error = (pred_value - exp_value)**2
errors.append(error)
return errors
def calculate_weight_adjustments(alpha, input, predicted_values, expected_values):
weight_adjustments = []
for pred_value, exp_value in zip(predicted_values, expected_values):
weight_adjustment = alpha * input * (pred_value- exp_value)
weight_adjustments.append(weight_adjustment)
return weight_adjustments
# calculate_updated_weights es exactamente la misma que en el escenario multi-entrada/salida-única
Con esas funciones en su lugar, la implementación final es mucho más simple
# Las funciones definidas arriba van aquí
input = 0.2
alpha = 24
expected_values = [8, 46, 0.1]
weights = [10, 20, 3]
while True:
# Debido a cómo python maneja punto flotante, redondeamos los valores
predicted_values = neural_network_multi_output(input, weights)
print("Según mi red neuronal, el 1er resultado es {}".format(predicted_values[0]))
print("Según mi red neuronal, el 2do resultado es {}".format(predicted_values[1]))
print("Según mi red neuronal, el 3er resultado es {}".format(predicted_values[2]))
errors = calculate_errors(predicted_values, expected_values)
print("El error en la 1ra predicción es {} ".format(errors[0]))
print("El error en la 2da predicción es {} ".format(errors[1]))
print("El error en la 3ra predicción es {} ".format(errors[2]))
weight_adjustments = calculate_weight_adjustments(alpha, input, predicted_values, expected_values)
weights = calculate_updated_weights(weights, weight_adjustments)
print("El nuevo valor de nuestro 1er peso es {}".format(weights[0]))
print("El nuevo valor de nuestro 2do peso es {}".format(weights[1]))
print("El nuevo valor de nuestro 3er peso es {}".format(weights[2]))
print("\n")
# Nos detenemos cuando todos los errores son 0
if(errors[0] + errors[1] + errors[2] == 0):
break
Ejecutar este código produce los mismos resultados que la implementación ingenua que listamos arriba, pero el código es mucho más fácil de entender y puede ejecutarse con cualquier número de salidas.
Una idea central con pequeños cambios
Como habrás notado, el descenso de gradiente cambia muy poco en los casos que acabamos de estudiar. La idea principal es que la topología de la red cambiará la forma en que calculamos el factor de ajuste para los pesos de la red neuronal.
Si aún no te sientes cómodo con estas ideas trata de re-implementar los ejemplos de código por tu cuenta. Entender cómo llegamos a la implementación final es un prerrequisito muy importante para el siguiente artículo de la serie: descenso de gradiente aplicado a redes neuronales con cualquier número de entradas y cualquier número de salidas.
¡Gracias por leer!
Qué hacer después
- Comparte este artículo con amigos y colegas. Gracias por ayudarme a llegar a personas que podrían encontrar útil esta información.
- Este artículo está basado en el libro: Grokking Deep Learning y en Deep Learning (Goodfellow, Bengio, Courville).
- Puedes encontrar el código fuente para esta serie aquí
- Envíame un email con preguntas, comentarios o sugerencias (está en la página Autor)
