In the previous article we learned what a neural network is and how it performs predictions: the input is combined with knowledge (in the form of a weight value) to produce an output.
In practice, just one input and one weight are rarely of any use. Most systems in the real world are much more complex, so you will need networks that can handle multiple inputs to solve current technological challenges.
Let's see how can we write a neural network that takes into consideration multiple pieces of data to achieve better estimations.
Informal linear algebra review: vectors and dot product
We can understand the intuition behind most machine learning topics with very little maths, but some concepts make things much easier to understand. For now, we only need two ideas: vectors and the dot product.
A vector is a list of numbers, represented by putting them between square brackets. Simple, right?
All these are vectors:
- [1 1] -> A vector with 2 elements
- [1 1 3 8] -> A vector with 4 elements
- [1 5 7 12 56984 5] -> A vector with 6 elements
The size of a vector is the number of elements it has. In the examples above, the vectors are of size 2, 4 and 6 (in descending order).
The dot product is an operation we perform on 2 vectors by grabbing the nth element of a vector and multiplying it for the nth element of the other vector. After we are done with the multiplications we sum the results and we are done. It's easier to understand with an example.
Suppose we have two vectors, [2 3 4] and [5 6 7]. We perform the dot product by:
- Multiplying the first element of each vectors: 2 * 5 = 10
- Multiplying the second element of each vectors: 3 * 6 = 18
- Multiplying the third element of each vector: 4 * 7 = 28
- Summing all the previous results 10+18+28 = 56
- The dot product of [2 3 4] and [4 5 7] is 56
It's important to remember that two vectors need to be of the same size for this operation to apply. You can't calculate the dot product of [1 2] and [2 3 4].
The dot product is an important thing to know if you want to learn more about machine learning. As an extra exercise, let's write a simple implementation of the dot product in Python:
def dot_product(first_vector, second_vector):
# Remember you can only use dot product on with the same size
assert( len(first_vector) == len(second_vector))
vectors_size = len(first_vector)
dot_product_result = 0
for index in range(vectors_size):
dot_product_result += first_vector[index] * second_vector[index]
return dot_product_result
This small demo helps you verify the above code works as expected:
test_vector_one = [2, 3, 4]
test_vector_two = [5, 6, 7]
test_dot_product = dot_product(test_vector_one, test_vector_two)
print("The result of the dot product between the two test vectors is: {}".format(test_dot_product) )
python3 dot_product_demo.py
The result of the dot product between the two test vectors is: 56
Good, now that we are done refreshing our linear algebra, let's go back to neural networks.
Multiple-input neural networks
We will continue working on the code for our neural network. Until now, it told us how many calories we burn after jogging a given amount of time.
Like any good engineer, we kept looking for ways to improve our model: We investigated and discovered that other factors influence how many calories we burn while jogging, like the speed (in m/s) and the runner's mass (in kg).
Neural networks can take into consideration multiple inputs to perform a prediction. Every input will have one specific weight associated with it, and the network will perform a weighted sum. The inputs will be multiplied by their respective weights, and the results will be summed together to produce the output.
In our previous example, a weight of 7.56 was applied to the minutes input. Our new neural network will have additional weights for speed and mass, for a total of 3 weights.
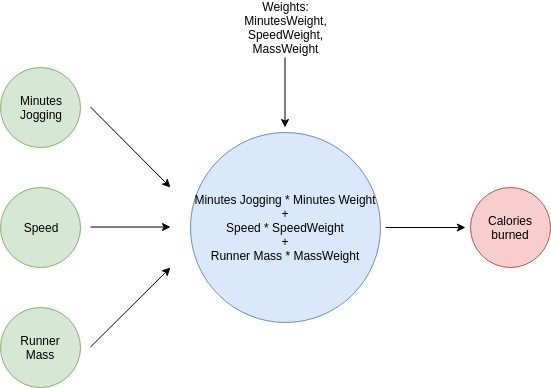
With mumbo-jumbo research, we discover that:
- The value of the weight associated with the number of minutes jogging is 6.2
- The value of the weight associated with the jogging speed 8.1
- The value of the weight associated with the mass of the runner is 0.31
This is the Python version of our calorie-prediction neural network:
# Now, input and information are both number arrays
def multi_input_neural_network(input_information, weights):
assert( len(input_information) == len(weights))
calories_burned = 0
for index in range(len(weights)):
calories_burned += input_information[index] * weights[index]
return calories_burned
We can also write a short demo to demonstrate how to use it:
#DEMO
# Inputs is an array, ordered as: minutes jogging --> jogging speed ---> mass of the runner
# Minutes jogging: 30
# Jogging speed: 3 m/s
# Runner's mass: 80kg
inputs = [30, 3, 80]
# The weights array follows the same order
calculated_weights = [6.2, 8.1, 0.31]
calories_burned = multi_input_neural_network(inputs, calculated_weights )
print("According to my neural network, I burned {} calories".format(calories_burned))
python3 multiple_input_nn.py
According to my neural network, I burned 235.10000000000002 calories
Wait a second, isn't that a dot product?
Yes, I'm glad you noticed.
If you pay attention to the implementation of the multi-input neural network, you will notice that the weighted sum is a dot product between the inputs and the weights.
Now that you noticed, we can re-implement our multi-input neural network using the dot-product function we implemented before:
def multi_input_neural_network(input_information, weights):
calories_burned = dot_product(input_information, weights)
return calories_burned
Nice and clean!
Note: In practice, you don't need to create your own implementations for the dot product or for neural networks. There are libraries with high-performance and well-tested implementations out there. Our implementations are meant to illustrate the principles, but creating your own machine learning library for production use is something you might not want to do just yet.
A bigger network: multiple inputs and multiple outputs
Neural networks can also output multiple estimates!
Previously, we learned how to combine multiple inputs with a vector of weights to create an estimate, something we can visualize as:
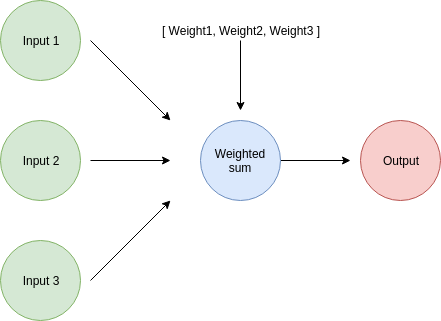
For estimating multiple outputs, we perform weighted sums with a different set of weights for every new output we need. Every prediction has its own associated vector of weights. For example, if we want to estimate 3 outputs, we need 3 sets of weights.
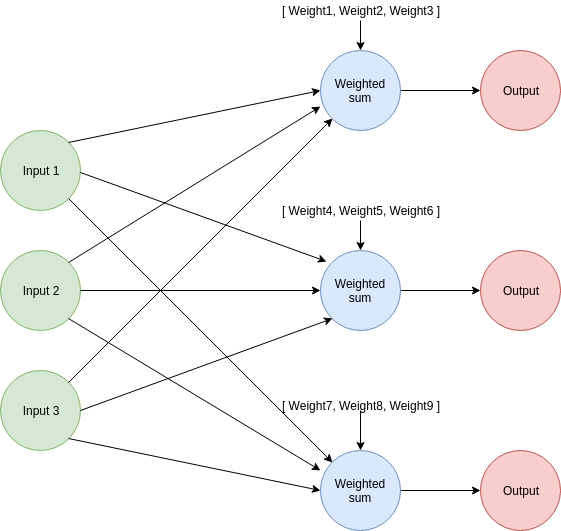
With this information, let's see how can we use this network to solve a practical problem. Suppose we want to use the info we already have to predict how many extra days I'll live thanks to my jogging sessions and how much money I'll save in medication, on top of the calories burned.
To summarize, our neural network now has:
Inputs:
- Number of minutes jogging
- Jogging speed
- Runner's mass
Outputs:
- Amount of calories burned
- Days of extended lifespan due to physical activity
- Money saved on heart medication.
Weights:
- A vector of weights for the estimation of calories.
- A vector of weights for the estimation of extra days.
- A vector of weights for the estimation of savings.
![]()
Three weighted sums will take place, one for each of the outputs. It may seem a bit complicated, but the implementation is straightforward once you understand what's going on.
def dot_product(first_vector, second_vector):
assert( len(first_vector) == len(second_vector))
vectors_size = len(first_vector)
dot_product_result = 0
for index in range(vectors_size):
dot_product_result += first_vector[index] * second_vector[index]
return dot_product_result
def multi_input_multi_output_neural_network(input_information, weights):
# Estimates will be put and returned in an array
estimates = []
for weights_for_estimate in weights:
estimates.append( dot_product(input_information, weights_for_estimate) )
return estimates
#DEMO
# Inputs is an array, ordered as: minutes jogging --> jogging speed ---> mass of the runner
# Minutes jogging: 30
# Jogging speed: 3 m/s
# Runner's mass: 80kg
inputs = [30, 3, 80]
# Weights for each of the 3 outputs
weights_for_calories = [6.2, 8.1, 0.31]
weights_for_extra_days = [0.00407, 0.00618, 0.00303]
weights_for_savings = [0.11, 0.23, 0.06]
# We combine all the weights in a single array to be fed in the neural network estimation function
all_weights = [weights_for_calories, weights_for_extra_days, weights_for_savings]
# The order of the results is the same as the order of weights calories -> extra days -> money saved
estimates = multi_input_multi_output_neural_network(inputs, all_weights )
print("According to my neural network, I burned {} calories".format(estimates[0]))
print("According to my neural network, I will live {} extra days".format(estimates[1]))
print("According to my neural network, I saved {} money units in hearth medication".format(estimates[2]))
Multiple input/output neural networks can seem a bit intimidating at first, but they are just extensions of things we already know. Most machine learning concepts are similar: at first, they seem complicated, but they are actually an amalgam of very simple underlying ideas.
I hope this article helped you understand neural networks with multiple inputs and outputs. Now that we know how the estimation process works, we can focus on learning the mechanisms networks use to tune the values of their weights.
What to do next
- Share this article with friends and colleagues. Thank you for helping me reach people who might find this information useful.
- You can find the source code for this series in this repo.
- This article is based on Grokking Deep Learning and on Deep Learning (Goodfellow, Bengio, Courville). These and other very helpful books can be found in the recommended reading list.
- Send me an email with questions, comments or suggestions (it's in the About Me page)