In the previous articles, we learned how neural networks perform estimations: a weighted sum is performed between the network inputs and its weights. Until now, the values of those weights were given to us by a mysterious external force. We took for granted that those are the values that produce the best estimates.
Finding the right value for each weight is a crucial step in deep learning: it's the process by which the network learns. At a very abstract level, you can see the network as a collection of weights that work together to produce predictions. We train the network by tweaking its weights until it predicts accurately.
In this chapter, we will learn a basic form of learning: hot/cold learning. The idea is extremely simple, but it's a good first step towards understanding more elaborate forms of learning.
Before proceeding, let's take another look at the process used by NNs to perform predictions.
Predicting, comparing, learning
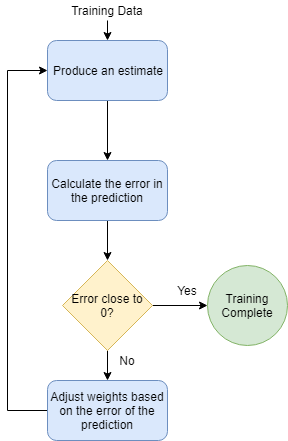
It's useful to imagine the process of training a neural network as 3 stages: estimation, comparison, and learning.
In the beginning, we have a collection of input and output values. It can be, for example, a spreadsheet that relates the number of minutes a person runs with the number of calories they burn. This is our training set, the one we will use to train the neural network.
The first step, estimation, is something we are already familiar with: an input is given to the neural network, which gets multiplied by the NN's weights and summed to produce an output.
The second step, comparison, gauges how good our prediction is. Suppose we know from our spreadsheet that running 20 minutes burns around 180 kcal. We give 20 as input to our neural network and it predicts we will burn 140 kcal. 180 is our expected value, the one we observe in real life and know is true, whereas 140 is the predicted value our network returned. These 2 pieces of information are enough to calculate the error. One way of doing it is substracting the expected value from the predicted one, and then calculating the absolute value of the result:
|140-180| = |-40| = 40
In this example, our error equals 40. This is an example of mean absolute error, and there are other ways of calculating the error in a prediction.
The third step, learning, is where update the weights of our neural network to improve the predictions. We use the error calculated in the previous step to decide how much we need to adjust the weights. It's important to note that if the error is 0 (or a number very close to 0) we can conclude our prediction is good enough and declare the learning process complete.
This is an iterative process: after adjusting the weights in the learning step, we start the cycle again. With the new weights, we produce a new prediction, calculate the error and if needed update the weights again, until our error gets small enough.
Weights can be adjusted in many different ways, in fact, most research in deep learning is focused on providing more effective ways of adjusting their values. For now, we will deal with one of the simplest ways: hot and cold learning.
Calculating the mean squared error
As mentioned before, we need a way to calculate how far from the expected values our predictions are. There are different forms of calculating this value: simple substractions, differences with absolute values, the distance between points in a plane, squared differences.
All these forms of calculating error prioritize different things. Mean squared error (we will learn about this later), for example, pays more attention to bigger errors and ignores small ones, while also ignoring the sign (positive or negative) of the error. Selecting the right way of calculating the error is important, as it determines how you evaluate the quality of your network's predictions.
The mean squared error (MSE) is a very popular way of calculating the error in different machine learning systems. The definition quite simple, suppose you have a collection inputs with their respective expected value, and you run the neural network to predict an estimated value for each of the inputs.
Then subtract the expected value to its respective estimated value, square the result, and in the end sum them all. As the last step, divide the result of the sum by the number of pairs.
The formula for MSE is:

Let's calculate it by hand once. Suppose we perform a series of estimates and tabulate the results:
| Input | Expected value | Estimated value |
|---|---|---|
| 2.1 | 11 | 13 |
| 4.0 | 23 | 19 |
| 22 | 45 | 52 |
We then calculate the MSE as:
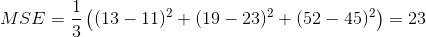
Easy, right?
You might have noticed that the results of the substractions are squared, this has the following interesting properties:
- All errors are positive: Because squaring a real number always gives a positive number as a result, the errors in MSE are always positive. This means that the information on the direction of the error (is it lower than expected or higher than expected) is lost. This is ok, because of the following property.
- Errors don't cancel each other: If we take into consideration the direction of the numbers and we make an aggregate of all of them, we might cancel some errors with others of opposite sign. If one estimate is off by -10000000 and the other is off by +10000000, our mean error would be 0, despite horrible mispredictions on both instances. A positive value for each error ensures they all contribute to the aggregate value.
- Big errors are emphasized over small ones: You might remember from high school that if the value is between 0 and 1, squaring it makes it smaller. This results in small errors (0 < errors < 1) to become even less significant and the bigger ones (errors > 1) to contribute more heavily. This is a good thing, as we can later concentrate on minimizing the biggest errors.
Hot and cold learning
Now that we understand error calculations, let's go back to learning.
In hot and cold learning, you just adjust weights up and down and see how the error changes. Essentially you keep increasing/decreasing the value of your weights until the error disappears or becomes very small.
Let's implement it stage by stage. In the beginning, we need a neural network that performs an estimate, it's also important to have an expected value to measure the error.
def neural_network(input, weight):
predicted_value = input * weight
return predicted_value
minutes_running = 20
actual_calories_burned = 180
# We perform this extra assignment just to keep consistency with the names
input = minutes_running
expected_value = actual_calories_burned
weight = 7
predicted_value = neural_network(input, weight)
print("According to my neural network, I burned {} calories".format(predicted_value))
If we run this code, it tells me I burned 140 calories. Let's calculate the error.
error = (predicted_value - expected_value)**2
print("The error in the prediction is {} ".format(error))
This tells us that the error in the estimation has a value of 1600 (MSE).
Now it's time to make little adjustments to the value of our weight and see how the error reacts. We will use a small value for our learning rate: a number we sum and subtract from our weight to see how the error changes.
With a rate of 0.1, we calculate errors for the weights 7.1 and 6.9. The one that produces the smaller error will become our new weight. This process is repeated until our error becomes 0 or gets very close to it.
learning_rate = 0.1
prediction_upwards = neural_network(input, weight + learning_rate)
error_upwards = (prediction_upwards - expected_value)**2
print("The prediction with an updated weight of {} has an error of {}".format(weight+learning_rate, error_upwards))
prediction_downwards = neural_network(input, weight - learning_rate)
error_downwards = (prediction_downwards - expected_value)**2
print("The prediction with an updated weight of {} has an error of {}".format(weight-learning_rate, error_downwards))
Our first run prints the following results:
The prediction with an updated weight of 7.1 has an error of 1444.0
The prediction with an updated weight of 6.9 has an error of 1764.0
As you can see, a weight with a value of 7.1 produces a smaller error value, so we update our weight to have that value.
Fully iterative demo
Hot and cold learning is an iterative process: we will continue updating weights until our error becomes very small. This fully-iterative demo does just that:
def neural_network(input, weight):
predicted_value = input * weight
return predicted_value
minutes_running = 20
actual_calories_burned = 180
# We perform this extra assignment just to keep consistency with the names
input = minutes_running
expected_value = actual_calories_burned
weight = 7
while True:
predicted_value = neural_network(input, weight)
print("According to my neural network, I burned {} calories".format(predicted_value))
error = (predicted_value - expected_value)**2
print("The error in the prediction is {} ".format(error))
learning_rate = 0.4
prediction_upwards = neural_network(input, weight + learning_rate)
error_upwards = (prediction_upwards - expected_value)**2
print("The prediction with an updated weight of {} has an error of {}".format(weight+learning_rate, error_upwards))
prediction_downwards = neural_network(input, weight - learning_rate)
error_downwards = (prediction_downwards - expected_value)**2
print("The prediction with an updated weight of {} has an error of {}".format(weight-learning_rate, error_downwards))
if(error_upwards < error_downwards):
weight = round(weight + learning_rate, 2)
else:
weight = round(weight - learning_rate, 2)
print("\n")
if(error == 0):
break
When you run it, this is what it prints:
According to my neural network, I burned 140 calories
The error in the prediction is 1600
The prediction with an updated weight of 7.4 has an error of 1024.0
The prediction with an updated weight of 6.6 has an error of 2304.0
According to my neural network, I burned 148.0 calories
The error in the prediction is 1024.0
The prediction with an updated weight of 7.800000000000001 has an error of 576.0
The prediction with an updated weight of 7.0 has an error of 1600.0
According to my neural network, I burned 156.0 calories
The error in the prediction is 576.0
The prediction with an updated weight of 8.2 has an error of 256.0
The prediction with an updated weight of 7.3999999999999995 has an error of 1024.0
According to my neural network, I burned 164.0 calories
The error in the prediction is 256.0
The prediction with an updated weight of 8.6 has an error of 64.0
The prediction with an updated weight of 7.799999999999999 has an error of 576.0000000000014
According to my neural network, I burned 172.0 calories
The error in the prediction is 64.0
The prediction with an updated weight of 9.0 has an error of 0.0
The prediction with an updated weight of 8.2 has an error of 256.0
According to my neural network, I burned 180.0 calories
The error in the prediction is 0.0
The prediction with an updated weight of 9.4 has an error of 64.0
The prediction with an updated weight of 8.6 has an error of 64.0
As you can see in the last 3 lines, any change to the weight of 9 will result in higher error values.
Be careful with the learning rate
A learning rate of 0.4 is much faster than a rate of 0.1 for finding a solution. If we increase the learning rate to 1, we can reach an error of 0 even faster:
According to my neural network, I burned 140 calories
The error in the prediction is 1600
The prediction with an updated weight of 8 has an error of 400
The prediction with an updated weight of 6 has an error of 3600
According to my neural network, I burned 160 calories
The error in the prediction is 400
The prediction with an updated weight of 9 has an error of 0
The prediction with an updated weight of 7 has an error of 1600
According to my neural network, I burned 180 calories
The error in the prediction is 0
The prediction with an updated weight of 10 has an error of 400
The prediction with an updated weight of 8 has an error of 400
Does that mean that a higher value will be even faster? well, yes, a value of 2 will be the fastest. But if you go above that, hot and cold learning will never produce a proper solution. The problem is that it will start oscillating between values that are far from 9, and it might never stop. Try it yourself and set the learning rate to 8, run the code and see how it eternally prints these lines:
...
According to my neural network, I burned 300 calories
The error in the prediction is 14400
The prediction with an updated weight of 23 has an error of 78400
The prediction with an updated weight of 7 has an error of 1600
According to my neural network, I burned 140 calories
The error in the prediction is 1600
The prediction with an updated weight of 15 has an error of 14400
The prediction with an updated weight of -1 has an error of 40000
According to my neural network, I burned 300 calories
The error in the prediction is 14400
The prediction with an updated weight of 23 has an error of 78400
The prediction with an updated weight of 7 has an error of 1600
According to my neural network, I burned 140 calories
The error in the prediction is 1600
The prediction with an updated weight of 15 has an error of 14400
The prediction with an updated weight of -1 has an error of 40000
...
A very low value for our learning rate will make our network slow but one that is too high would make it unusable. This, and the fact that hot and cold learning is usually very slow, is the reason this is never used in production.
Still, it's a very good way of understanding the basics of a NN's learning process, something I hope is much more clear to you after reading this article. In the next article, we will learn about a more powerful form of learning: gradient descent.
Thank you for reading!
What to do next
- Share this article with friends and colleagues. Thank you for helping me reach people who might find this information useful.
- You can find the source code for this series in this repo.
- This article is based on Grokking Deep Learning and on Deep Learning (Goodfellow, Bengio, Courville). These and other very helpful books can be found in the recommended reading list.
- Send me an email with questions, comments or suggestions (it's in the About Me page)