In the previous article the foundations for a generalized implementation of gradient descent. Namely, cases with multiple inputs and one output, and multiple outputs and one input.
In this article, we will continue our generalization efforts to come up with a version of gradient descent that works with any number of inputs and outputs.
First, we will create a step-by-step implementation for just 3 inputs and 3 outputs. From this, we will extrapolate another implementation that supports any number of inputs and outputs.
Gradient descent: Multiple inputs - multiple outputs.
The generalized gradient descent for a network with multiple inputs uses a combination of the approaches used in the two previous cases.
- Like the multiples input/1-output case, you will perform corrections to individual weights by multiplying their respective inputs by a common factor
alpha * (predicted_value - expected_value). - Like the 1-input/multiple outputs case, you can visualize every one of those weight-output subsystems as individual neural networks.
It's all about calculating an adjustment factor for every weight using the right values. Every weight adjustment calculation must only involve only values (input, expected value, predicted value) related to its particular weight.
Step-by-step implementation of a 3x3 network
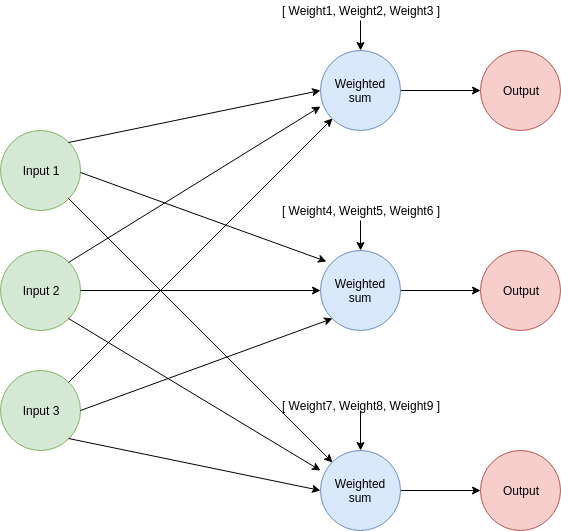
Take a look at the diagram if you are having trouble picturing the parts of the network.
For our implementation:
- We will set up the needed variables and have a weight-adjustment loop, just as we did in all previous cases.
- In the first part of the optimization loop, we will calculate the predictions for all the outputs. Next, we will calculate the error in each prediction using the respective expected values.
- We will calculate the weight adjustment factor for each of our 9 weights and perform the required adjustments.
- We will check if the error values add up to 0 (or very close to 0). With this information, we can decide if our predictions are good enough or if we need to keep the optimization loop running.
As mentioned before, we will perform the predictions and adjustments as if we were dealing with 3 subnetworks with the same input values.
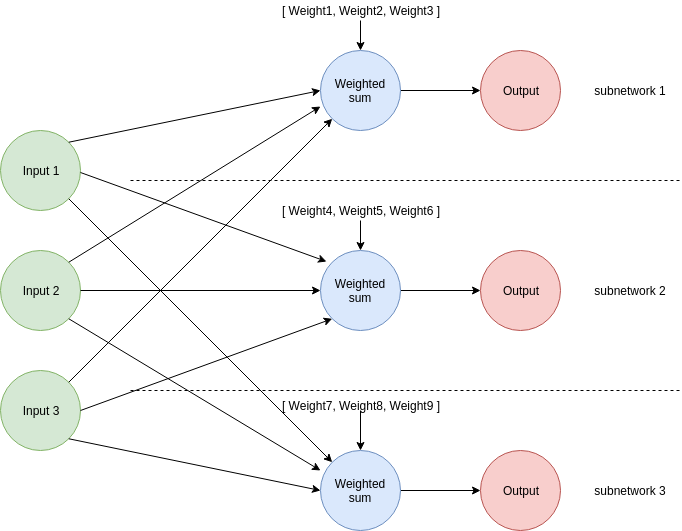
Variables setup
The first step is creating our variables:
alpha = 0.2
inputs = [0.2, 2.3, 1.2]
expected_values = [8, 46, 0.1]
weights_1 = [7.1, 1.1, 4.4] # Weights for the first output
weights_2 = [5.7, 3, 9.1] # Weights for the second output
weights_3 = [2.2, 5.3, 7] # Weights for the third output
weights = [weights_1, weights_2, weights_3]
The order is important: The first entry in the expected values corresponds to the first expected value. Also, notice that we put all weights in a two-dimensional array. As you imagined, the first 3 weights produce the first output (related to the first expected/predicted value), and so on.
Prediction and error calculation
Now it's time for the prediction and error calculation steps. We will write a multi-output neural network function to calculate each of the outputs.
# In previous articles we explained how this works
def dot_product(first_vector, second_vector):
assert( len(first_vector) == len(second_vector))
vectors_size = len(first_vector)
dot_product_result = 0
for index in range(vectors_size):
dot_product_result += first_vector[index] * second_vector[index]
return round(dot_product_result, 2)
def multi_input_multi_output_neural_network(inputs, weights):
predicted_values= []
for weights_for_estimate in weights:
predicted_values.append( dot_product(inputs, weights_for_estimate) )
return predicted_values
#...
#This happens inside of the weight-updating loop
predicted_values = multi_input_multi_output_neural_network(inputs, weights)
error_1 = (predicted_values[0] - expected_values[0])**2
error_2 = (predicted_values[1] - expected_values[1])**2
error_3 = (predicted_values[2] - expected_values[2])**2
The prediction function performs the same operations we already know: it grabs the weights that belong to the first sub-network (the uppermost in the picture) and estimates the first output. Afterward, it performs the same operation for the 2nd and 3rd subnetworks. Every output (predicted value) is put in the returned array in the order they were calculated.
This order is important for keeping consistency in our calculations. As a result we can calculate every error as error_N = (predicted_values[N] - expected_values[N])**2.
Now we can deal with the weight adjustment part using the formulas we already know.
Adjusting weights
Remember we calculated the new value of a weight as:
weight -= alpha * input * (predicted_value - expected_value)
Let's recap what these mean:
- alpha is a learning rate that helps us regulate the speed of learning and prevent overshooting.
- input is the value of the input that was multiplied by the weight we are currently updating.
- predicted_value is the output our weight participated in producing.
- expected_value is the expected value associated with the predicted_value.
Applying gradient descent for neural networks with multiple inputs and outputs is just a matter of applying that equation to every weight in the network using the right values.
Let's see the code for the adjustment of the weights for the first sub-network:
weight_adjustment_1 = alpha * inputs[0] * (predicted_values[0] - expected_values[0])
weight_adjustment_2 = alpha * inputs[1] * (predicted_values[0] - expected_values[0])
weight_adjustment_3 = alpha * inputs[2] * (predicted_values[0] - expected_values[0])
weights[0][0] -= weight_adjustment_1
weights[0][1] -= weight_adjustment_2
weights[0][2] -= weight_adjustment_3
The code is pretty self-explanatory, but pay attention to the following details:
- Because our weights are placed in a two-dimensional array, we use the first index (in this case 0) to specify which set of weights we are working with. The second index tells us the specific weight. For example
weights[0][0]means first sub-network, first weight. - The weight_adjustment factor uses the input that its respective weight multiplied when producing the output.
- alpha is the same for everyone.
- The equations use only the first (index 0) values for predicted value and expected value because those are the ones predicted and expected by the first sub-network.
Let's look now at the second (middle) subnetwork weight adjustment process:
weight_adjustment_4 = alpha * inputs[0] * (predicted_values[1] - expected_values[1])
weight_adjustment_5 = alpha * inputs[1] * (predicted_values[1] - expected_values[1])
weight_adjustment_6 = alpha * inputs[2] * (predicted_values[1] - expected_values[1])
weights[1][0] -= weight_adjustment_4
weights[1][1] -= weight_adjustment_5
weights[1][2] -= weight_adjustment_6
- Notice that the first index when referring to the weights variable is 1. This means that we are now dealing with the 2nd sub-network.
- The weight_adjustment factor uses the input that its respective weight multiplied when producing the output.
- alpha is still the same.
- The equations use only the second (index 1) values for predicted value and expected value because those are the ones predicted and expected by the second sub-network.
Now that you get an idea of what multiplied by the right values means, you can understand what's going on with the last 3 weights in our neural network.
weight_adjustment_7 = alpha * inputs[0] * (predicted_values[2] - expected_values[2])
weight_adjustment_8 = alpha * inputs[1] * (predicted_values[2] - expected_values[2])
weight_adjustment_9 = alpha * inputs[2] * (predicted_values[2] - expected_values[2])
weights[2][0] -= weight_adjustment_7
weights[2][1] -= weight_adjustment_8
weights[2][2] -= weight_adjustment_9
Deciding when to stop
We still keep the same criteria for success: adjust the values of our weights until the error values are 0 or close to 0. The simplest way of finding out if we are successful is by adding all errors and checking if they are 0. If they are, we can break the cycle:
if(error_1 + error_2 + error_3 == 0):
break
Putting it all together
The final implementation of our 3-input/3-output neural network looks like this:
def dot_product(first_vector, second_vector):
assert( len(first_vector) == len(second_vector))
vectors_size = len(first_vector)
dot_product_result = 0
for index in range(vectors_size):
dot_product_result += first_vector[index] * second_vector[index]
return round(dot_product_result, 2)
def multi_input_multi_output_neural_network(inputs, weights):
predicted_values= []
for weights_for_estimate in weights:
predicted_values.append( dot_product(inputs, weights_for_estimate) )
return predicted_values
alpha = 0.2
inputs = [0.2, 2.3, 1.2]
expected_values = [8, 46, 0.1]
weights_1 = [7.1, 1.1, 4.4] # Weights for the first output
weights_2 = [5.7, 3, 9.1] # Weights for the second output
weights_3 = [2.2, 5.3, 7] # Weights for the third output
weights = [weights_1, weights_2, weights_3]
while True:
predicted_values = multi_input_multi_output_neural_network(inputs, weights)
print("According to my neural network, the 1st result is {}".format(predicted_values[0]))
print("According to my neural network, the 2nd result is {}".format(predicted_values[1]))
print("According to my neural network, the 3rd result is {}".format(predicted_values[2]))
error_1 = (predicted_values[0] - expected_values[0])**2
error_2 = (predicted_values[1] - expected_values[1])**2
error_3 = (predicted_values[2] - expected_values[2])**2
print("The error in the 1st prediction is {} ".format(error_1))
print("The error in the 2nd prediction is {} ".format(error_2))
print("The error in the 3rd prediction is {} ".format(error_3))
## These weights participated in the prediction of the first output value
weight_adjustment_1 = alpha * inputs[0] * (predicted_values[0] - expected_values[0])
weight_adjustment_2 = alpha * inputs[1] * (predicted_values[0] - expected_values[0])
weight_adjustment_3 = alpha * inputs[2] * (predicted_values[0] - expected_values[0])
weights[0][0] -= weight_adjustment_1
weights[0][1] -= weight_adjustment_2
weights[0][2] -= weight_adjustment_3
print("\n")
print("The 1st weight for the first output is now {} ".format(weights[0][0]) )
print("The 2nd weight for the first output is now {} ".format(weights[0][1]) )
print("The 3rd weight for the first output is now {} ".format(weights[0][2]) )
## These weights participated in the prediction of the second output value
weight_adjustment_4 = alpha * inputs[0] * (predicted_values[1] - expected_values[1])
weight_adjustment_5 = alpha * inputs[1] * (predicted_values[1] - expected_values[1])
weight_adjustment_6 = alpha * inputs[2] * (predicted_values[1] - expected_values[1])
weights[1][0] -= weight_adjustment_4
weights[1][1] -= weight_adjustment_5
weights[1][2] -= weight_adjustment_6
print("\n")
print("The 1st weight for the second output is now {} ".format(weights[1][0]) )
print("The 2nd weight for the second output is now {} ".format(weights[1][1]) )
print("The 3rd weight for the second output is now {} ".format(weights[1][2]) )
## These weights participated in the prediction of the third output value
weight_adjustment_7 = alpha * inputs[0] * (predicted_values[2] - expected_values[2])
weight_adjustment_8 = alpha * inputs[1] * (predicted_values[2] - expected_values[2])
weight_adjustment_9 = alpha * inputs[2] * (predicted_values[2] - expected_values[2])
weights[2][0] -= weight_adjustment_7
weights[2][1] -= weight_adjustment_8
weights[2][2] -= weight_adjustment_9
print("\n")
print("The 1st weight for the third output is now {} ".format(weights[2][0]) )
print("The 2nd weight for the third output is now {} ".format(weights[2][1]) )
print("The 3rd weight for the third output is now {} ".format(weights[2][2]) )
print("\n")
#We stop when all errors are 0
if(error_1 + error_2 + error_3 == 0):
break
You can verify this network works by running the code and checking your terminal:
According to my neural network, the 1st result is 9.23
According to my neural network, the 2nd result is 18.96
According to my neural network, the 3rd result is 21.03
The error in the 1st prediction is 1.512900000000001
The error in the 2nd prediction is 731.1615999999999
The error in the 3rd prediction is 438.06489999999997
The 1st weight for the first output is now 7.0508
The 2nd weight for the first output is now 0.5341999999999999
The 3rd weight for the first output is now 4.1048
The 1st weight for the second output is now 6.7816
The 2nd weight for the second output is now 15.438399999999998
The 3rd weight for the second output is now 15.589599999999999
The 1st weight for the third output is now 1.3628
The 2nd weight for the third output is now -4.327799999999999
The 3rd weight for the third output is now 1.9768
According to my neural network, the 1st result is 7.56
According to my neural network, the 2nd result is 55.57
According to my neural network, the 3rd result is -7.31
The error in the 1st prediction is 0.19360000000000036
The error in the 2nd prediction is 91.5849
The error in the 3rd prediction is 54.90809999999999
The 1st weight for the first output is now 7.0684
The 2nd weight for the first output is now 0.7366
The 3rd weight for the first output is now 4.2104
The 1st weight for the second output is now 6.3988
The 2nd weight for the second output is now 11.036199999999997
The 3rd weight for the second output is now 13.2928
The 1st weight for the third output is now 1.6592
The 2nd weight for the third output is now -0.9191999999999996
The 3rd weight for the third output is now 3.7551999999999994
... More iterations
According to my neural network, the 1st result is 8.0
According to my neural network, the 2nd result is 46.0
According to my neural network, the 3rd result is 0.1
The error in the 1st prediction is 0.0
The error in the 2nd prediction is 0.0
The error in the 3rd prediction is 0.0
The 1st weight for the first output is now 7.063599999999999
The 2nd weight for the first output is now 0.6814000000000001
The 3rd weight for the first output is now 4.1816
The 1st weight for the second output is now 6.498799999999999
The 2nd weight for the second output is now 12.186199999999996
The 3rd weight for the second output is now 13.8928
The 1st weight for the third output is now 1.5816
The 2nd weight for the third output is now -1.8115999999999994
The 3rd weight for the third output is now 3.2895999999999996
Step-by-step implementation of a generalized network
Generalizing for any number of inputs and outputs can be done by grabbing our basic 3x3 implementation and refactoring it to work with vectors. We can do this by creating functions that operate on collections of elements instead of applying the equations one-by-one.
Variables setup
Our variable setup doesn't need any change, as they are all put into vectors already. Let's pat ourselves on the back for being forward-thinkers and understanding the importance of collections.
Prediction and error calculation
The prediction part doesn't need any updates. We are using a generalized prediction function that works with any number of inputs and outputs, so there's nothing to change there.
For the error calculation, we need to create a function that receives an array of predicted values and expected values and returns a new array with the errors:
def calculate_errors(predicted_values, expected_values):
errors = []
for predicted_value, expected_value in zip(predicted_values, expected_values):
error = (predicted_value - expected_value)**2
errors.append(error)
return errors
#...
# Our previous 3 lines are now just one
errors = calculate_errors(predicted_values, expected_values)
Adjusting weights
The weight adjustment process has two main parts:
- Calculating the weight adjustment factors for every weight.
- Substracting every adjustment factor from its respective weight.
This is easier to visualize in matrix form: Imagine we have a matrix of weights and a matrix of adjustment factors. Updating the weights is just a matter of calculating the second matrix and subtracting it from the first one.
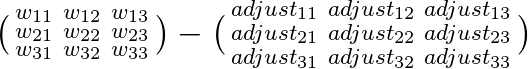
The values for the adjustment matrices are not secret, we already calculated them in our first implementation. The only difference is that instead of calculating them one-by-one, we will calculate them in a 2d-array. In our 3x3 example, the adjustment matrix looks like this:
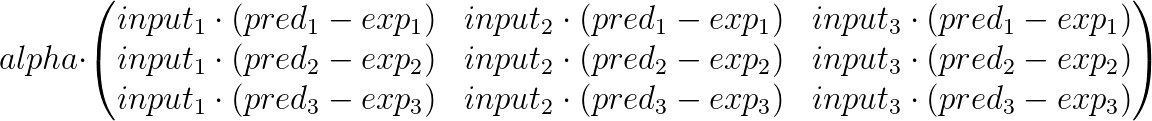
This matrix is just an arrangement of the correction values we calculated one by one in the first implementation. Some things that might help you understand it a bit better are:
- Notice that alpha is multiplying every single entry in the matrix.
- Every row represents the correction values associated with a single output. That's why the first row only deals with the expected and predicted values for the first output and so on.
- Every column is multiplied by a specific input, all weights in that column were multiplied by that input for producing a prediction.
- If you increase the number of inputs the matrix becomes wider if you increase the number of outputs it becomes taller.
We just need to implement a function that calculates these values when given alpha, an array for expected values and an array of predicted values and inputs:
def calculate_weight_correction_matrix(alpha, inputs, expected_values, predicted_values):
weight_correction_factors = []
#Calculates factors row for row
for exp, pred in zip(expected_values, predicted_values):
row = []
delta = (pred - exp) * alpha
for input in inputs:
row.append( input * delta )
weight_correction_factors.append(row)
return weight_correction_factors
The next step is easier, we just need to create a function that substracts this correction factor matrix from the weight matrix:
def calculate_corrected_weights(weights, correction_factors):
updated_weights = []
for row_weight, row_correction in zip(weights, correction_factors):
row = []
for weight, correction in zip(row_weight, row_correction):
row.append( weight - correction )
updated_weights.append(row)
return updated_weights
With this in place, all the previous lines for correcting weight values can be reduced to just two. What's more, we are not limited to 3x3 neural networks anymore:
weight_correction_factors = calculate_weight_correction_matrix(alpha, inputs, expected_values, predicted_values)
weights = calculate_corrected_weights(weights, weight_correction_factors)
Next, deciding when to stop.
Deciding when to stop
This is another easy implementation: we just need a function that returns the sum of every weight in the errors array.
def calculate_total_error(errors):
return sum(errors)
# ...
if(calculate_total_error(errors) == 0):
break
Done!
Putting it all together
After applying all the changes, this is the final version of the code:
def dot_product(first_vector, second_vector):
assert( len(first_vector) == len(second_vector))
vectors_size = len(first_vector)
dot_product_result = 0
for index in range(vectors_size):
dot_product_result += first_vector[index] * second_vector[index]
return round(dot_product_result, 2)
def multi_input_multi_output_neural_network(inputs, weights):
predicted_values= []
for weights_for_estimate in weights:
predicted_values.append( dot_product(inputs, weights_for_estimate) )
return predicted_values
def calculate_errors(predicted_values, expected_values):
errors = []
for predicted_value, expected_value in zip(predicted_values, expected_values):
error = (predicted_value - expected_value)**2
errors.append(error)
return errors
def calculate_weight_correction_matrix(alpha, inputs, expected_values, predicted_values):
weight_correction_factors = []
#Calculates factors row for row
for exp, pred in zip(expected_values, predicted_values):
row = []
delta = (pred - exp) * alpha
for input in inputs:
row.append( input * delta )
weight_correction_factors.append(row)
return weight_correction_factors
def calculate_corrected_weights(weights, correction_factors):
updated_weights = []
for row_weight, row_correction in zip(weights, correction_factors):
row = []
for weight, correction in zip(row_weight, row_correction):
row.append( weight - correction )
updated_weights.append(row)
return updated_weights
def calculate_total_error(errors):
return sum(errors)
alpha = 0.2
inputs = [0.2, 2.3, 1.2]
expected_values = [8, 46, 0.1]
weights_1 = [7.1, 1.1, 4.4] # Weights for the first output
weights_2 = [5.7, 3, 9.1] # Weights for the second output
weights_3 = [2.2, 5.3, 7] # Weights for the third output
weights = [weights_1, weights_2, weights_3]
while True:
predicted_values = multi_input_multi_output_neural_network(inputs, weights)
print("According to my neural network, the 1st result is {}".format(predicted_values[0]))
print("According to my neural network, the 2nd result is {}".format(predicted_values[1]))
print("According to my neural network, the 3rd result is {}".format(predicted_values[2]))
errors = calculate_errors(predicted_values, expected_values)
print("The error in the 1st prediction is {} ".format(errors[0]))
print("The error in the 2nd prediction is {} ".format(errors[1]))
print("The error in the 3rd prediction is {} ".format(errors[2]))
## These weights participated in the prediction of the first output value
weight_correction_factors = calculate_weight_correction_matrix(alpha, inputs, expected_values, predicted_values)
weights = calculate_corrected_weights(weights, weight_correction_factors)
print("\n")
print("The 1st weight for the first output is now {} ".format(weights[0][0]) )
print("The 2nd weight for the first output is now {} ".format(weights[0][1]) )
print("The 3rd weight for the first output is now {} ".format(weights[0][2]) )
print("\n")
print("The 1st weight for the second output is now {} ".format(weights[1][0]) )
print("The 2nd weight for the second output is now {} ".format(weights[1][1]) )
print("The 3rd weight for the second output is now {} ".format(weights[1][2]) )
print("\n")
print("The 1st weight for the third output is now {} ".format(weights[2][0]) )
print("The 2nd weight for the third output is now {} ".format(weights[2][1]) )
print("The 3rd weight for the third output is now {} ".format(weights[2][2]) )
print("\n")
#We stop when all errors are 0
if(calculate_total_error(errors) == 0):
break
Running this code will produce the same results as our first version. The upside is that now we have an implementation of gradient descent that can deal with any number of inputs and outputs!
Now you know gradient descent
If you made it this far, congratulations!
In the last three articles, we explored (dissected) gradient descent. It might seem overly complicated in the beginning, but it's an incredibly powerful technique with a huge array of applications in data science and machine learning.
This article is quite big and dense, but if you made it this far you already have a much better understanding of gradient descent. I tried to go be step-by-step as possible, something that hopefully made the article easier to understand.
Now that most of the groundwork has been laid, we can start dealing with more deep-learning-y stuff.
Thank you for reading!
What to do next
- Share this article with friends and colleagues. Thank you for helping me reach people who might find this information useful.
- You can find the source code for this series in this repo.
- This article is based on Grokking Deep Learning and on Deep Learning (Goodfellow, Bengio, Courville). These and other very helpful books can be found in the recommended reading list.
- Send me an email with questions, comments or suggestions (it's in the About Me page)